When analyzing a graph, accurately describing the function it represents is crucial. By understanding the function’s behavior, we can gain insights into the underlying data and make informed decisions. In this article, we will explore the various statements that describe a graph’s function, enabling you to confidently identify the correct description.

1. Identifying the Type of Function
Linear Function: A linear function is represented by a straight line and can be expressed as f(x) = mx + b, where m is the slope and b is the y-intercept.
Quadratic Function: A quadratic function is represented by a parabola and can be expressed as f(x) = ax^2 + bx + c, where a, b, and c are constants.
Polynomial Function: A polynomial function is represented by a curve and can be expressed as f(x) = a_nx^n + a_{n-1}x^{n-1} + ... + a_1x + a_0, where a_n, a_{n-1}, …, a_1, and a_0 are constants.
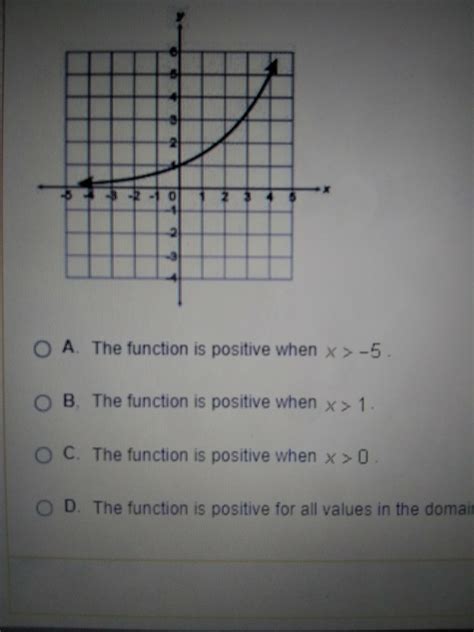
Exponential Function: An exponential function is represented by a curve that increases or decreases rapidly and can be expressed as f(x) = a^x, where a is a positive constant.
Logarithmic Function: A logarithmic function is represented by a curve that is the inverse of an exponential function and can be expressed as f(x) = log_a(x), where a is a positive constant.
2. Describing the Function’s Characteristics
Once you have identified the type of function, you can further describe its characteristics:
Increasing Function: A function is increasing if its values increase as the input increases.
Decreasing Function: A function is decreasing if its values decrease as the input increases.
Constant Function: A function is constant if its value remains the same for all inputs.
Maximum Value: The maximum value of a function is the highest point on its graph.
Minimum Value: The minimum value of a function is the lowest point on its graph.
3. Common Mistakes to Avoid
When describing a graph’s function, avoid these common mistakes:
- Mistaking a quadratic function for a linear function.
- Not recognizing the domain and range of the function.
- Confusing increasing and decreasing intervals.
- Misidentifying the maximum or minimum value.
4. How to Describe a Function’s Graph
To accurately describe a function’s graph, follow these steps:
- Identify the type of function (linear, quadratic, etc.).
- Determine whether the function is increasing, decreasing, or constant.
- Identify the maximum and minimum values (if any).
- Describe the domain and range of the function.
5. Useful Tables
| Function Type | Equation | Behavior |
|---|---|---|
| Linear | f(x) = mx + b |
Straight line |
| Quadratic | f(x) = ax^2 + bx + c |
Parabola |
| Exponential | f(x) = a^x |
Rapid increase or decrease |
| Logarithmic | f(x) = log_a(x) |
Inverse of exponential function |
6. Creative New Word
Functionographer: A person who analyzes and describes functions represented by graphs.
7. FAQs
Q: How can I determine the type of function just by looking at the graph?
A: Examine the shape of the graph and look for characteristics such as linearity, parabolic shape, or exponential growth/decay.
Q: What is the difference between an increasing and a decreasing function?
A: An increasing function’s values grow as the input increases, while a decreasing function’s values shrink as the input increases.
Q: Can a function have multiple maximum or minimum values?
A: Yes, a function can have multiple local maximums and minimums, but only one global maximum and one global minimum.
Q: Why is it important to describe a function’s domain and range?
A: Knowing the domain and range helps define the input and output values for which the function is valid.
Conclusion
By understanding the different ways to describe a graph’s function, you can effectively communicate its behavior and characteristics. Whether you are a student, researcher, or data analyst, accurately describing functions is essential for comprehending and interpreting mathematical and scientific information.