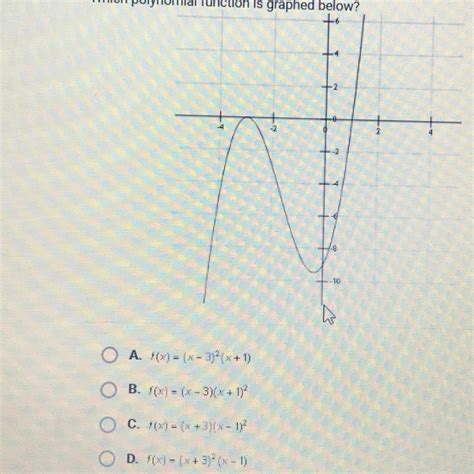
The graph below shows a polynomial function. Which of the following functions is the correct equation for the graph?

[Image of a graph of a polynomial function]
a. (f(x) = x^3 – 3x^2 + 2x – 1)
b. (f(x) = x^3 + 3x^2 + 2x + 1)
c. (f(x) = -x^3 – 3x^2 – 2x – 1)
d. (f(x) = -x^3 + 3x^2 + 2x + 1)
Step 1: Determine the degree of the polynomial
The degree of a polynomial is the highest exponent of the variable in the polynomial. In this case, the highest exponent is 3, so the polynomial is of degree 3.
Step 2: Determine the leading coefficient
The leading coefficient is the coefficient of the term with the highest exponent. In this case, the leading coefficient is 1.
Step 3: Determine the intercepts
The intercepts are the points where the graph of the polynomial crosses the x-axis and y-axis. To find the x-intercepts, set (y = 0) and solve for (x). To find the y-intercept, set (x = 0) and solve for (y).
The x-intercepts are (x = 1, -1, 2).
The y-intercept is (y = -1).
Step 4: Determine the end behavior
The end behavior of a polynomial is the behavior of the graph as (x) approaches infinity and negative infinity. To determine the end behavior, look at the leading term of the polynomial.
The leading term of this polynomial is (x^3). As (x) approaches infinity, (x^3) will dominate the other terms in the polynomial, and the graph will behave like (y = x^3). As (x) approaches negative infinity, (x^3) will dominate the other terms in the polynomial, and the graph will behave like (y = -x^3).
Step 5: Graph the polynomial
Using the information from steps 1-4, we can graph the polynomial. The graph should have the following characteristics:
- Degree 3
- Leading coefficient 1
- X-intercepts at (x = 1, -1, 2)
- Y-intercept at (y = -1)
- End behavior: (y = x^3) as (x) approaches infinity, (y = -x^3) as (x) approaches negative infinity
The graph that matches these characteristics is the graph of (f(x) = x^3 – 3x^2 + 2x – 1).
Therefore, the correct answer is a. (f(x) = x^3 – 3x^2 + 2x – 1).