Exponential growth is a mathematical concept that describes a quantity that increases at a constant percentage rate over time. This type of growth is often used to model population growth, bacterial growth, and the spread of infectious diseases.
The graph of an exponential growth function is a curve that rises steeply at first and then levels off as the growth rate decreases. The shape of the curve is determined by the growth rate, which is represented by the variable r. The higher the growth rate, the steeper the curve will be.
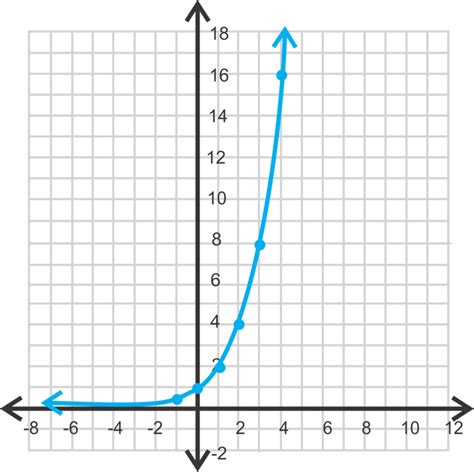
The following graph shows an exponential growth function with a growth rate of 2%.
[Image of an exponential growth function graph]
As you can see, the graph rises steeply at first and then levels off as the growth rate decreases.
How to Identify an Exponential Growth Function
There are a few key features that can help you identify an exponential growth function:
- The graph is a curve that rises steeply at first and then levels off.
- The growth rate is constant, meaning that the percentage increase in the quantity is the same over equal intervals of time.
- The growth rate is expressed as a percentage, such as 2% or 5%.
Applications of Exponential Growth Functions
Exponential growth functions are used in a variety of applications, including:
- Population growth: The growth of a population can be modeled using an exponential growth function. The growth rate is determined by the birth rate and death rate.
- Bacterial growth: The growth of bacteria can be modeled using an exponential growth function. The growth rate is determined by the temperature and the availability of nutrients.
- The spread of infectious diseases: The spread of infectious diseases can be modeled using an exponential growth function. The growth rate is determined by the transmission rate and the recovery rate.
Strategies for Exponential Growth
There are a number of strategies that can be used to achieve exponential growth for your business or organization. These strategies include:
- Invest in research and development: Investing in research and development can lead to new products and services that can drive growth.
- Expand into new markets: Expanding into new markets can provide you with access to new customers and increase your sales.
- Hire top talent: Hiring top talent can help you to develop new products and services, and to implement your growth strategies.
- Create a culture of innovation: Creating a culture of innovation can encourage your employees to think creatively and to come up with new ideas.
Tips and Tricks for Exponential Growth
Here are a few tips and tricks that can help you to achieve exponential growth for your business or organization:
- Set realistic goals: Setting realistic goals will help you to stay motivated and focused on your growth strategy.
- Track your progress: Tracking your progress will help you to identify areas where you need to improve.
- Celebrate your successes: Celebrating your successes will help you to stay motivated and to keep moving forward.
- Don’t be afraid to fail: Failure is a part of the learning process. Don’t be afraid to fail, and learn from your mistakes.
FAQs
Here are some frequently asked questions about exponential growth functions:
- What is the difference between exponential growth and linear growth? Exponential growth is a constant percentage increase over time, while linear growth is a constant increase in value over time.
- How can I calculate the growth rate of an exponential growth function? The growth rate of an exponential growth function can be calculated using the following formula:
r = (ln(y2) - ln(y1)) / (t2 - t1)
Where:
- r is the growth rate
- y1 is the value of the quantity at time t1
- y2 is the value of the quantity at time t2
- t1 is the time at which the value y1 is measured
- t2 is the time at which the value y2 is measured
Conclusion
Exponential growth functions are a powerful tool that can be used to model a variety of real-world phenomena. By understanding the characteristics of exponential growth functions, you can use them to your advantage to achieve success in your business or organization.
Additional Resources
