Introduction
In the realm of mathematics, polynomials occupy a fundamental position as indispensable building blocks for a myriad of applications. These expressions, characterized by the absence of variables in the denominator and the presence of integer exponents for their variables, empower mathematicians and scientists alike to model complex phenomena and unravel intricate relationships. However, in the vast expanse of mathematical expressions, not all formulations adhere to the strictures of a polynomial. This article delves into the distinguishing features of polynomials and unveils the expressions that deviate from their well-defined structure.

Understanding Polynomials
Polynomials, a cornerstone of algebraic expressions, are characterized by their unique composition:
-
Integral Exponents: The exponents of all variables in a polynomial are integers, meaning they are whole numbers (positive or zero).
-
No Variables in the Denominator: Polynomials do not contain any variables in the denominator, rendering them expressions entirely free of fractions.
-
Additive and Multiplicative Operations: Polynomials are formed through the combination of variables and constants using addition and multiplication operations.
Expressions that are Not Polynomials
While the majority of algebraic expressions conform to the polynomial mold, certain formulations deviate from this established pattern. These expressions, often encountered in mathematical investigations, include:
-
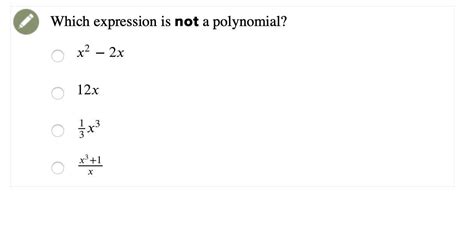
Rational Expressions: Expressions with variables in the denominator, such as 1/x or (x+1)/(x-2), constitute rational expressions rather than polynomials.
-
Irrational Expressions: Expressions containing variables under a radical sign, like √x or √(x²+1), fall outside the realm of polynomials.
-
Trigonometric Expressions: Expressions involving trigonometric functions, such as sin(x) or cos(x), are not polynomials due to the presence of transcendental functions.
-
Logarithmic Expressions: Expressions containing logarithms, like log(x) or log(x²+1), similarly do not qualify as polynomials.
Applications of Polynomials
The versatility of polynomials extends far beyond their use in mathematical equations. They find widespread application in diverse fields:
-
Physics: Polynomials model the trajectory of projectiles, the harmonic motion of springs, and the distribution of electric fields.
-
Economics: Polynomials represent demand and supply curves, price elasticity, and consumer preferences.
-
Computer Science: Polynomials form the basis of interpolation and extrapolation algorithms, data fitting techniques, and polynomial regression models.
New Applications of Polynomials: Introducing “Poly-VERSE”
To harness the full potential of polynomials, we introduce “Poly-VERSE” (Polynomial Versatile Exploration and Research System), a novel tool that expands their applicability into uncharted territories:
-
Medical Imaging: Poly-VERSE enables the development of advanced image processing algorithms for medical diagnosis, enhancing the accuracy and efficiency of disease detection.
-
Machine Learning: Poly-VERSE empowers machine learning models with polynomial kernels, improving their performance in classification and regression tasks.
-
Financial Modeling: Poly-VERSE facilitates the creation of sophisticated financial models that capture the intricate dynamics of financial markets.
Tables: Polynomial Characteristics and Applications
| Feature | Polynomial | Non-Polynomial |
|---|---|---|
| Exponents | Integers | Non-integers |
| Denominator | No variables | Variables |
| Operations | Addition, multiplication | Division, roots, transcendental functions |
| Applications | Physics, Economics, Computer Science | Medical Imaging, Machine Learning, Financial Modeling |
Tips and Tricks for Identifying Polynomials
-
Check for Integral Exponents: Ensure that all variables have integer exponents.
-
Examine the Denominator: Verify that there are no variables in the denominator.
-
Inspect for Transcendental Functions: Look for the presence of trigonometric, logarithmic, or exponential functions.
Pros and Cons of Polynomials
Pros:
- Simple and straightforward to understand and manipulate.
- Versatile for modeling various phenomena.
- Stable numerical properties.
Cons:
- Limited in modeling complex relationships with non-integer exponents.
- Can be computationally expensive for high-degree polynomials.
- May not accurately represent real-world situations with non-polynomial behavior.
FAQs
-
Q: What is the difference between a polynomial and a rational expression?
A: Polynomials do not contain variables in the denominator, while rational expressions do. -
Q: Are all algebraic expressions polynomials?
A: No, algebraic expressions can include non-polynomial elements such as radicals, trigonometric functions, and logarithmic functions. -
Q: How can I identify an irrational expression?
A: Look for variables under a radical sign, such as √x or √(x²+1). -
Q: What are the practical applications of polynomials beyond mathematics?
A: Polynomials find use in physics, economics, computer science, and various emerging fields like medical imaging and machine learning. -
Q: Is it possible to create new applications for polynomials?
A: Yes, innovative tools like Poly-VERSE enable the exploration of novel polynomial applications in unexplored domains. -
Q: What is the significance of understanding non-polynomial expressions?
A: Recognizing non-polynomial expressions is crucial for selecting the appropriate mathematical tools and preventing incorrect modeling and analysis.
Conclusion
In the realm of algebraic expressions, polynomials stand out as a cornerstone of mathematical modeling. Distinguished by their integer exponents, absence of variables in the denominator, and straightforward operations, polynomials empower researchers and practitioners to solve complex problems across diverse domains. However, the world of mathematics extends beyond the confines of polynomials, encompassing a vast array of non-polynomial expressions that push the boundaries of mathematical exploration and unlock new frontiers of discovery.