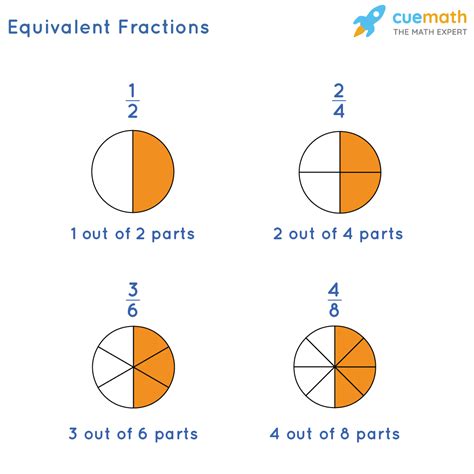
In mathematics, fractions represent parts of a whole. They are written in the form a/b, where a is the numerator and b is the denominator. The numerator tells us how many parts we have, while the denominator tells us how many equal parts make up the whole.

Understanding 9/12 as a Fraction
The fraction 9/12 represents nine equal parts out of a total of twelve parts. This means that if we divide a whole into twelve equal pieces, 9/12 of it would represent nine of those pieces.
Finding Equivalent Fractions
An equivalent fraction has the same value as the original fraction. We can find equivalent fractions by multiplying or dividing both the numerator and the denominator by the same nonzero number.
Multiplying Both Numerator and Denominator
To find an equivalent fraction by multiplying, we can use the following formula:
(a/b) * (c/d) = (a * c)/(b * d)
Using this formula, we can find an equivalent fraction for 9/12 by multiplying both the numerator and the denominator by 3:
(9/12) * (3/3) = (9 * 3)/(12 * 3) = 27/36
Dividing Both Numerator and Denominator
Similarly, we can find an equivalent fraction by dividing both the numerator and the denominator by the same nonzero number. Using the same formula as before:
(a/b) * (c/d) = (a * c)/(b * d)
We can find an equivalent fraction for 9/12 by dividing both the numerator and the denominator by 3:
(9/12) * (1/3) = (9 * 1)/(12 * 3) = 9/36
Applications of Equivalent Fractions
Equivalent fractions have various applications in real-world scenarios, including:
-
Comparing Fractions: Equivalent fractions allow us to compare the size of different fractions. For example, we can say that 9/12 is equivalent to 27/36, which means that both fractions represent the same amount of a whole.
-
Simplifying Fractions: By finding equivalent fractions with a smaller denominator, we can simplify fractions to make them easier to work with. For instance, we can simplify 9/12 to 3/4 by multiplying both the numerator and the denominator by 3.
-
Solving Equations: Equivalent fractions can be used to solve equations that involve fractions. By substituting one equivalent fraction for another, we can simplify the equation and find the solution.
-
Measuring and Comparing: Equivalent fractions are useful for measuring and comparing different quantities. For example, in a recipe, we may need to divide an ingredient into equal parts. By using equivalent fractions, we can ensure that each part is the same size.
Common Mistakes to Avoid
When working with fractions, it is important to avoid common mistakes, such as:
-
Forgetting to Multiply or Divide: Always remember to multiply or divide both the numerator and the denominator when finding equivalent fractions.
-
Changing the Value of the Fraction: When simplifying fractions, make sure that the equivalent fraction has the same value as the original fraction.
-
Mixing Units: When measuring or comparing different quantities, ensure that the units are consistent across the equivalent fractions.
Why Equivalent Fractions Matter
Equivalent fractions are essential for understanding and working with fractions effectively. They allow us to compare, simplify, solve equations, and measure quantities accurately. By comprehending the concept of equivalent fractions, we can enhance our mathematical problem-solving abilities.
Benefits of Understanding Equivalent Fractions
Understanding equivalent fractions offers numerous benefits, including:
-
Improved Fraction Manipulation: Equivalent fractions make it easier to manipulate fractions by allowing us to convert them into different forms with the same value.
-
Enhanced Fraction Comparison: By recognizing equivalent fractions, we can quickly compare the size of fractions and determine their relative values.
-
Simplified Fraction Calculations: Equivalent fractions simplify fraction calculations by reducing complex fractions to simpler forms, making them easier to work with.
-
Increased Problem-Solving Skills: Understanding equivalent fractions enables us to solve fraction-related problems efficiently and accurately.
FAQs
1. What is the simplest form of 9/12?
The simplest form of 9/12 is 3/4, which is obtained by dividing both the numerator and the denominator by 3.
2. How do you find equivalent fractions for a given fraction?
To find equivalent fractions, multiply or divide both the numerator and the denominator by the same nonzero number.
3. Why is it important to understand equivalent fractions?
Understanding equivalent fractions is essential for comparing, simplifying, solving equations, and measuring quantities involving fractions.
4. Can you provide an example of how equivalent fractions are used in real life?
Equivalent fractions are used in culinary recipes to ensure that ingredients are divided into equal portions or when comparing the prices of items sold in different units.
5. What are some common mistakes to avoid when working with equivalent fractions?
Common mistakes include forgetting to multiply or divide both the numerator and denominator, changing the value of the fraction, or mixing units when comparing different quantities.
6. How can I improve my understanding of equivalent fractions?
Practice finding equivalent fractions, comparing fractions using equivalent forms, and solving fraction-related problems to solidify your comprehension.
Tables
Table 1: Equivalent Fractions for 9/12
| Equivalent Fraction |
|—|—|—|
| 9/12 |
| 27/36 |
| 18/24 |
| 3/4 |
Table 2: Applications of Equivalent Fractions
| Application | Description |
|---|---|
| Comparing Fractions | Determining the relative size of different fractions |
| Simplifying Fractions | Reducing fractions to smaller, equivalent forms |
| Solving Equations | Substituting equivalent fractions to simplify equations |
| Measuring and Comparing | Ensuring equal portions or comparing quantities |
Table 3: Common Mistakes to Avoid with Equivalent Fractions
| Mistake | Description |
|---|---|
| Forgetting to Multiply or Divide | Failing to multiply or divide both the numerator and denominator when finding equivalent fractions |
| Changing the Value of the Fraction | Altering the value of the original fraction when simplifying |
| Mixing Units | Using different units when comparing equivalent fractions, leading to incorrect results |
Table 4: Benefits of Understanding Equivalent Fractions
| Benefit | Description |
|---|---|
| Improved Fraction Manipulation | Facilitating the conversion and manipulation of fractions |
| Enhanced Fraction Comparison | Enabling quick and accurate comparison of fraction sizes |
| Simplified Fraction Calculations | Reducing the complexity of fraction calculations |
| Increased Problem-Solving Skills | Enhancing the ability to solve fraction-related problems effectively |