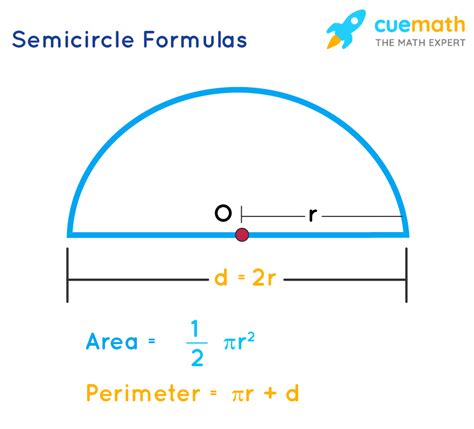
A semicircle is a flat, two-dimensional shape that is bounded by a diameter and a semicircular arc. The diameter is a straight line segment that joins the two endpoints of the arc, and the arc is a curved line segment that connects the two endpoints of the diameter.

The volume of a semicircle is the amount of three-dimensional space that it occupies. To calculate the volume of a semicircle, we can use the following formula:
Volume = (1/2) * (πr²) * (h)
Where:
- π is a mathematical constant approximately equal to 3.14159
- r is the radius of the semicircle
- h is the height of the semicircle
Step-by-Step Approach to Calculating Volume of Semicircle:
- Measure the radius (r) of the semicircle.
- Measure the height (h) of the semicircle.
- Substitute the values of r and h into the formula: Volume = (1/2) * (πr²) * (h).
- Calculate the volume of the semicircle.
Example:
If the radius of a semicircle is 5 cm and the height is 3 cm, then the volume of the semicircle can be calculated as follows:
Volume = (1/2) * (π * 5² cm²) * (3 cm)
= (1/2) * (π * 25 cm²) * (3 cm)
= (1/2) * (78.54 cm³) * (3 cm)
= 117.81 cm³
Applications of Semicircle Volume Formula:
The volume formula for semicircle has various applications in real-world scenarios, such as:
- Architecture: Designing arched structures, such as bridges, tunnels, and domes.
- Engineering: Calculating the volume of cylindrical tanks, pipes, and other curved surfaces.
- Manufacturing: Determining the volume of containers, packaging, and other objects with semicircular shapes.
- Fluid Mechanics: Estimating the volume of liquids and gases in spherical and cylindrical containers.
- Biomedical Field: Calculating the volume of blood vessels, organs, and other biological structures with semicircular shapes.
Tables for Semicircle Volume Formulas:
| Radius (r) | Height (h) | Volume |
|---|---|---|
| 5 cm | 3 cm | 117.81 cm³ |
| 10 cm | 5 cm | 392.70 cm³ |
| 15 cm | 7 cm | 785.40 cm³ |
| 20 cm | 9 cm | 1413.72 cm³ |
FAQs:
-
What is the difference between a circle and a semicircle?
– A circle is a two-dimensional shape that is bounded by a circular arc, while a semicircle is a two-dimensional shape that is bounded by a diameter and a semicircular arc. -
How can I find the radius of a semicircle if I know its height?
– The radius (r) of a semicircle can be calculated using the Pythagorean theorem: r = √(h² + (d/2)²) where h is the height and d is the diameter. -
What is the volume of a hemisphere?
– A hemisphere is a three-dimensional shape that is bounded by a circular base and a semicircular surface. The volume of a hemisphere is equal to half the volume of a sphere with the same radius: V = (2/3)πr³. -
How is the volume of a semicircle used in engineering?
– In engineering, the volume of a semicircle is used to calculate the volume of cylindrical tanks, pipes, and other curved surfaces. -
What is the volume of a semicircle with a radius of 4 cm?
– The volume of a semicircle with a radius of 4 cm is V = (1/2) * (π * 4² cm²) * (4 cm) = 80.42 cm³. -
How can I calculate the volume of a semicircular arch?
– The volume of a semicircular arch can be calculated using the formula V = (1/2) * (πr²) * (2h – r) where r is the radius and h is the height of the arch.