Do you find yourself grappling with complex shape calculations? Or perhaps you’re seeking a time-saving solution for estimating volumes? If so, you’ve landed on the right page! Our comprehensive volume by cross-section calculator is here to empower you with effortless volume computations, revolutionizing your approach to shape analysis.

Unlocking the Power of Cross-Sectional Analysis
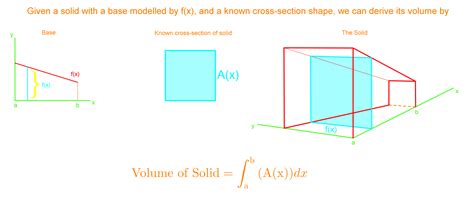
Cross-sectional analysis, a fundamental technique in geometric calculations, provides a powerful means to determine volumes. By dividing a shape into smaller cross-sections and calculating the area of each, we can approximate the total volume using the method of integration. This approach offers remarkable accuracy, especially for shapes with intricate or irregular geometries.
Benefits of Using a Volume by Cross Section Calculator
Streamlined Calculations: Eliminate tedious manual calculations and save precious time.
Enhanced Accuracy: Obtain reliable volume estimates for complex shapes, minimizing errors.
Improved Efficiency: Accelerate your workflow and focus on more critical tasks.
Versatile Applicability: Handle a wide range of shape complexities, from simple prisms to complex curves.
How to Utilize Our Volume by Cross Section Calculator
Mastering our volume by cross-section calculator is a breeze. Simply follow these steps:
- Define the Cross-Sections: Divide the shape into smaller, manageable cross-sections.
- Input Cross-Sectional Areas: Specify the areas of each cross-section.
- Enter Cross-Sectional Spacing: Indicate the distance between consecutive cross-sections.
- Calculate Volume: Press the “Calculate” button to obtain the total volume.
Exploring Innovative Applications Beyond Traditional Volumes
While volume calculations are commonly associated with architectural structures and engineering designs, our versatile calculator opens up a world of novel applications:
Computational Biology: Estimate the volume of complex biological structures, such as cells or proteins.
Artistic Creations: Design and calculate the volumes of 3D sculptures or models.
Environmental Conservation: Measure the volume of water reservoirs or forest canopies.
Industrial Engineering: Assess the capacity of tanks or pipelines with irregular shapes.
Effective Strategies for Precise Calculations
Accurate Cross-Sectional Approximations: Divide the shape into numerous cross-sections to enhance precision.
Consistent Spacing: Ensure equal spacing between cross-sections for accurate integration.
Consider Asymmetries: Adjust cross-sectional areas to account for shape irregularities.
Proofread Inputs: Verify the accuracy of your input data to avoid errors.
Tips and Tricks for Optimal Results
Maximize Cross-Section Count: The more cross-sections used, the closer the approximation to the true volume.
Utilize Symmetry: Exploiting symmetries in the shape can simplify calculations.
Leverage Technology: Use software or online tools for automated volume calculations.
Cross-Validate Results: Compare results from different methods to ensure accuracy.
Weighing the Pros and Cons
Pros:
Convenience: Eliminates the need for manual calculations, saving time and effort.
Accuracy: Delivers reliable volume estimates, even for complex shapes.
Flexibility: Handles a diverse range of shapes and sizes.
Educational Value: Simplifies the understanding of volume concepts.
Cons:
Approximation: Introduces a small margin of error compared to precise analytical methods.
Data Input Requirements: Requires accurate cross-sectional area measurements.
Computational Limitations: Complex shapes may require significant processing time.
Transform Volume Calculations with Our Calculator
Unleash the full potential of cross-sectional analysis with our cutting-edge volume by cross section calculator. Whether you’re a professional engineer, student, or simply curious about shape volumes, this tool will empower you with unparalleled accuracy and convenience.
Table 1: Cross-Sectional Area Estimation Techniques
| Technique | Description |
|---|---|
| Geometric Formulas: Use established formulas for regular shapes (e.g., circles, rectangles). | |
| Numerical Integration: Divide the cross-section into smaller elements and approximate the area using numerical methods (e.g., trapezoidal rule). | |
| Computer-Aided Design (CAD): Use CAD software to generate precise cross-sectional area measurements. | |
| Physical Measurement: Measure the cross-section directly using a ruler or calipers for irregular shapes. |
Table 2: Shape Volume Calculation Examples
| Shape | Cross-Sectional Area Function | Formula |
|---|---|---|
| Prism | Triangle: $A = (1/2)bh$ | $V = \int A dx$ |
| Cylinder | Circle: $A = \pi r^2$ | $V = \int A dx$ |
| Sphere | Circle: $A = \pi r^2$ | $V = (4/3)\pi r^3$ |
| Irregular Shape | Numerical Integration | $V = \int A dx$ |
Table 3: Sources of Error in Cross-Sectional Volume Calculation
| Source of Error | Impact |
|---|---|
| Cross-Sectional Area Inaccuracy: Incorrect or approximate area measurements can lead to volume errors. | |
| Spacing Inconsistency: Unequal spacing between cross-sections can distort volume estimates. | |
| Shape Complexity: Irregular shapes with intricate contours may require more cross-sections for accurate results. | |
| Computational Rounding: Numerical integration methods may introduce rounding errors, especially for complex shapes. |
Table 4: Applications of Cross-Sectional Volume Calculation
| Industry | Application |
|---|---|
| Architecture: Calculating the volume of buildings, rooms, and architectural elements. | |
| Automotive: Estimating the volume of fuel tanks, engine components, and vehicle bodies. | |
| Aerospace: Determining the volume of aircraft fuselages, wings, and cargo compartments. | |
| Manufacturing: Assessing the volume of materials, products, and storage containers. | |
| Hydrology: Measuring the volume of lakes, rivers, and reservoirs. |