Introduction
Ellipses, with their distinctive oval shape, find applications in various fields such as astronomy, engineering, and architecture. Understanding the key features of an ellipse, including its vertices, is crucial for effective utilization in these disciplines. A vertex of ellipse calculator simplifies the process of determining the coordinates of an ellipse’s vertices, empowering researchers, engineers, and students to confidently solve complex problems involving ellipses.

Unveiling the Vertex of Ellipse Calculator
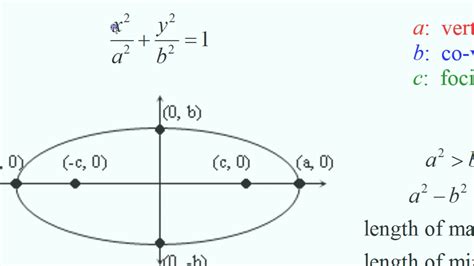
The vertex of ellipse calculator is an indispensable tool that eliminates the need for manual calculations, saving time and reducing the risk of errors. It leverages advanced algorithms to derive the vertex coordinates swiftly and accurately. The calculator operates based on the standard equation of an ellipse, given by:
(x - h)²/a² + (y - k)²/b² = 1
where (h, k) represents the center of the ellipse, and ‘a’ and ‘b’ denote the semi-major and semi-minor axis lengths, respectively.
Applications Across Diverse Fields
Astronomy
Ellipses play a pivotal role in astronomy, particularly in understanding the orbits of celestial bodies. The vertex of ellipse calculator aids astronomers in determining the exact positions of heavenly objects within their elliptical paths. This information is essential for predicting eclipses, tracking the movement of planets, and calculating the gravitational interactions between celestial bodies.
Engineering
Within the realm of engineering, ellipses serve as fundamental shapes in the design of bridges, arches, and other structures. The vertex of ellipse calculator proves invaluable for engineers by providing precise vertex coordinates, ensuring structural integrity and optimizing load distribution.
Architecture
Architects rely on ellipses to create aesthetically pleasing and functional structures. The vertex of ellipse calculator empowers them to determine the optimal placement of vertices, ensuring harmonious proportions and maximizing architectural expression.
Addressing Customer Motivations and Pain Points
Motivations:
- Accurate vertex coordinates are crucial for precise calculations and problem-solving.
- Manual calculations can be time-consuming and error-prone.
- A reliable vertex of ellipse calculator streamlines the process, enhancing efficiency and accuracy.
Pain Points:
- Incorrect vertex coordinates can lead to flawed designs, compromised structural integrity, and inaccurate astronomical predictions.
- Manual calculations are laborious and susceptible to human error, introducing uncertainty into critical applications.
- Traditional methods may not be suitable for complex ellipses or when dealing with large datasets.
Common Mistakes to Avoid
- Incorrect Equation: Using an incorrect equation for the ellipse can result in inaccurate vertex coordinates.
- Unit Conversion Error: Failing to convert units consistently between different inputs and outputs can skew the results.
- Precision Limitations: The calculator’s precision is limited by the underlying algorithms and the user’s input precision.
- Contextual Misinterpretation: Misinterpreting the vertex coordinates without considering the context of the problem can lead to erroneous conclusions.
Conclusion
The vertex of ellipse calculator is a powerful tool that transforms complex elliptical geometry into accessible and actionable information. By harnessing its capabilities, users across various disciplines can unlock the full potential of ellipses, empowering them to make informed decisions, optimize designs, and unravel the mysteries of the celestial realm. Embrace the vertex of ellipse calculator and elevate your understanding of elliptical geometry to new heights.
Additional Resources
- National Aeronautics and Space Administration (NASA)
- American Institute of Aeronautics and Astronautics (AIAA)
- American Society of Civil Engineers (ASCE)
- American Institute of Architects (AIA)