Introduction: Unveiling the Secrets of the Unit Circle
Trigonometry, the study of triangles, is a cornerstone of mathematics, physics, and engineering. At its heart lies the enigmatic unit circle, a geometrical tool that unlocks the secrets of trigonometric functions. This comprehensive cheat sheet provides an in-depth exploration of the unit circle, empowering you to navigate the complexities of trigonometry with ease.

Understanding the Unit Circle
The unit circle, often denoted as S^1, is a circle with a radius of 1. It is centered at the origin of a two-dimensional Cartesian coordinate system (x, y). The unit circle serves as a graphical representation of trigonometric functions, allowing us to visualize and analyze their behavior.
Special Points on the Unit Circle
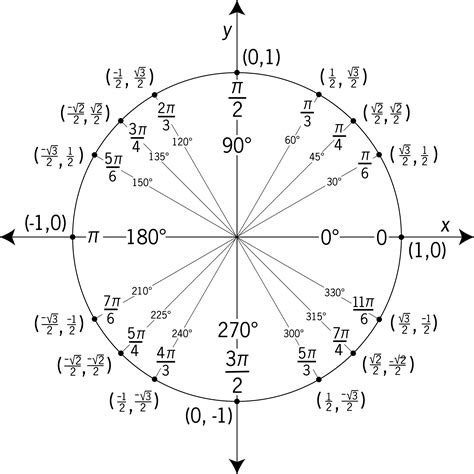
The unit circle contains several special points that have significant trigonometric values:
- (1, 0): Where the x-axis intersects the circle, representing the angle 0°.
- (0, 1): Where the y-axis intersects the circle, representing the angle 90°.
- (-1, 0): Where the x-axis intersects the circle on the negative side, representing the angle 180°.
- (0, -1): Where the y-axis intersects the circle on the negative side, representing the angle 270°.
Properties of the Unit Circle
The unit circle exhibits several fundamental properties:
- Circumference: 2π
- Area: π
- Radius: 1
- Equation: x^2 + y^2 = 1
Trigonometric Functions and the Unit Circle
Trigonometric functions (sine, cosine, tangent, cotangent, secant, and cosecant) are defined as ratios of the coordinates of points on the unit circle. By studying the positions of these points, we can determine the values of trigonometric functions for any angle.
Sine and Cosine Functions
- Sine (sin θ): The y-coordinate of the point on the unit circle corresponding to angle θ.
- Cosine (cos θ): The x-coordinate of the point on the unit circle corresponding to angle θ.
Tangent and Cotangent Functions
- Tangent (tan θ): The ratio of the y-coordinate to the x-coordinate of the point on the unit circle corresponding to angle θ.
- Cotangent (cot θ): The ratio of the x-coordinate to the y-coordinate of the point on the unit circle corresponding to angle θ.
Secant and Cosecant Functions
- Secant (sec θ): The reciprocal of the cosine function, representing the length of the hypotenuse of the right triangle formed by the point on the unit circle and the x- and y-axes.
- Cosecant (csc θ): The reciprocal of the sine function, representing the length of the hypotenuse of the right triangle formed by the point on the unit circle and the y-axis.
Applications of the Unit Circle
The unit circle finds myriad applications in various scientific and engineering fields:
- Navigation: Calculating angles and distances in navigation systems.
- Physics: Determining the trajectory of projectiles, pendulums, and other objects in motion.
- Engineering: Designing antennas, radars, and other electrical devices.
- Computer Graphics: Generating 3D models, animations, and textures.
- Medical Imaging: Processing medical images, such as MRI scans and CT scans.
Unit Circle Cheat Sheet: Key Values
Trigonometric Functions of Special Angles
| Angle (θ) | Sine (sin θ) | Cosine (cos θ) | Tangent (tan θ) | Cotangent (cot θ) | Secant (sec θ) | Cosecant (csc θ) |
|---|---|---|---|---|---|---|
| 0° | 0 | 1 | 0 | Undefined | 1 | Undefined |
| 30° | 1/2 | √3/2 | 1/√3 | √3 | 2/√3 | 2 |
| 45° | √2/2 | √2/2 | 1 | 1 | √2 | √2 |
| 60° | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
| 90° | 1 | 0 | Undefined | 0 | Undefined | 1 |
| 120° | √3/2 | -1/2 | -√3 | -1/√3 | -2/√3 | 2 |
| 135° | √2/2 | -√2/2 | -1 | -1 | -√2 | √2 |
| 150° | 1/2 | -√3/2 | -1/√3 | √3 | -2/√3 | 2 |
| 180° | 0 | -1 | 0 | Undefined | -1 | Undefined |
| 210° | -1/2 | -√3/2 | 1/√3 | √3 | -2/√3 | -2 |
| 225° | -√2/2 | -√2/2 | 1 | 1 | -√2 | -√2 |
| 240° | -√3/2 | -1/2 | √3 | 1/√3 | -2/√3 | -2 |
| 270° | -1 | 0 | Undefined | 0 | Undefined | -1 |
| 300° | -√3/2 | 1/2 | -√3 | -1/√3 | -2/√3 | -2 |
| 315° | -√2/2 | √2/2 | -1 | -1 | -√2 | -√2 |
| 330° | -1/2 | √3/2 | -1/√3 | √3 | -2/√3 | -2 |
| 360° | 0 | 1 | 0 | Undefined | 1 | Undefined |
Advanced Applications: Beyond the Basics
Parametric Equations of the Unit Circle
The unit circle can be described parametrically using the sine and cosine functions:
- x = cos θ
- y = sin θ
Polar Coordinates
The unit circle also serves as the basis for polar coordinates, a system used to represent points in a plane using their distance from the origin and the angle they make with the positive x-axis:
- r = distance from the origin
- θ = angle with the positive x-axis
Frequently Asked Questions (FAQs)
-
What is the significance of the unit circle in trigonometry?
– The unit circle provides a graphical representation of trigonometric functions, allowing for easy visualization and analysis of their behavior. -
How can I find the sine and cosine of an angle using the unit circle?
– Locate the point on the unit circle corresponding to the angle and read its y-coordinate (sine) and x-coordinate (cosine). -
Is it possible to find the values of trigonometric functions for angles greater than 360°?
– Yes, by adding or subtracting multiples of 360° from the angle. -
How can I use the unit circle to solve real-world problems?
– By applying trigonometric relationships to scenarios involving angles, distances, and heights. -
What are some advanced applications of the unit circle?
– Parametric equations, polar coordinates, and Fourier analysis. -
How can I memorize the values of trigonometric functions for special angles?
– Use mnemonic devices, such as SOHCAHTOA (sine = opposite/hypotenuse, cosine = adjacent/hypotenuse, tangent = opposite/adjacent).
Conclusion: Unlocking the Power of Trigonometry
The unit circle is a fundamental tool in trigonometry, providing a geometric framework for understanding and applying trigonometric functions. This comprehensive cheat sheet serves as an invaluable resource for students, researchers, and professionals alike, empowering them to navigate the complexities of trigonometry with confidence and accuracy. By understanding the properties, applications, and key values associated with the unit circle, the secrets of trigonometry are unlocked, paving the way for deeper exploration and practical applications.