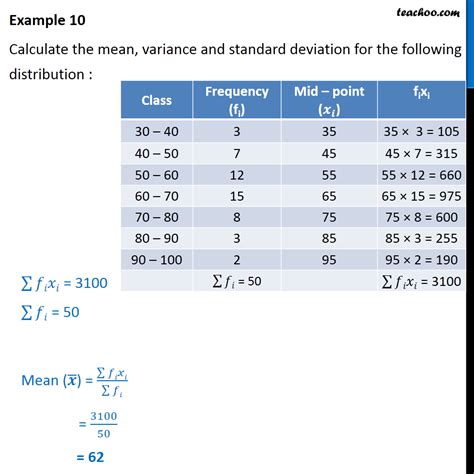
What is the Relationship Between the Variance and Standard Deviation?

The variance and standard deviation are two important statistical measures that are often used together to describe the spread of a data set. The variance is a measure of how much the data is spread out, while the standard deviation is a measure of how much the data is spread out around the mean.

The variance and standard deviation are related by the following equation:

Standard deviation = square root of variance

This means that the standard deviation is always the square root of the variance.

The variance and standard deviation can be calculated using the following formulas:

Variance:

Variance = (1/n) * sum((x - mean)^2)

where:

• n is the number of data points
• x is a data point
• mean is the mean of the data set

Standard deviation:

Standard deviation = square root of variance

Let’s say we have the following data set:

1, 2, 3, 4, 5

The mean of this data set is 3. The variance is 2. The standard deviation is 1.41.

The variance and standard deviation are used in a wide variety of applications, including:

• Quality control: The variance and standard deviation can be used to monitor the quality of a product or process.
• Financial analysis: The variance and standard deviation can be used to analyze the risk and return of an investment.
• Medical research: The variance and standard deviation can be used to analyze the effectiveness of a treatment or drug.

When using the variance and standard deviation, it is important to avoid the following common mistakes:

• Confusing the variance with the standard deviation. The variance is a measure of how much the data is spread out, while the standard deviation is a measure of how much the data is spread out around the mean.
• Using the variance or standard deviation to make inferences about a population. The variance and standard deviation are only measures of the spread of a data set. They cannot be used to make inferences about a population.
• Using the variance or standard deviation to compare data sets with different means. The variance and standard deviation are not comparable across data sets with different means.

The variance and standard deviation are two important statistical measures that can be used to describe the spread of a data set. They are used in a wide variety of applications, including quality control, financial analysis, and medical research. When using the variance and standard deviation, it is important to avoid the common mistakes listed above.

• Variance and Standard Deviation
• Variance and Standard Deviation Calculator
• The Difference Between Variance and Standard Deviation