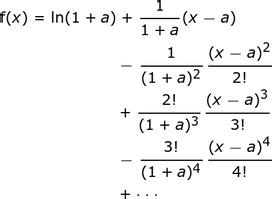Introduction
The natural logarithm, often denoted as ln(x), plays a pivotal role in various scientific and mathematical disciplines. However, calculating its value can be computationally expensive, especially for complex expressions involving fractional or negative exponents. The Taylor series expansion offers an elegant solution to this challenge, enabling us to approximate ln(1 + x) with a desired level of accuracy.

Taylor Series for ln(1 + x)
The Taylor series expansion of ln(1 + x) around x = 0 is given by:
ln(1 + x) = x - x²/2 + x³/3 - x⁴/4 + ...
where … denotes higher-order terms. This series converges for |x| < 1.
Applications of the Taylor Series Expansion
The Taylor series expansion for ln(1 + x) finds numerous applications in diverse fields, including:
Approximation of Logarithmic Functions
The Taylor series expansion provides a convenient way to approximate ln(1 + x) for small values of x. For example, if |x| < 0.5, the first three terms of the series, namely:
ln(1 + x) ≈ x - x²/2 + x³/3
suffice to yield a highly accurate approximation.
Derivatives and Integrals
The derivatives of ln(1 + x) can be easily obtained by differentiating the Taylor series term by term. Similarly, the integral of ln(1 + x) can be found by integrating the Taylor series term by term.
Series Acceleration
The Taylor series expansion can be used as a starting point for more sophisticated series acceleration techniques, which aim to enhance the convergence rate of the series.
Numerical Analysis
The Taylor series expansion for ln(1 + x) is frequently employed in numerical analysis for solving equations, approximating functions, and performing error analysis.
Computational Implementation
The Taylor series expansion for ln(1 + x) can be efficiently implemented using computer code. Here is a Python snippet that calculates the approximate value of ln(1.2) using the first three terms of the series:
import math
x = 0.2
terms = 3
# Initialize the approximation
approximation = x
# Add successive terms to the approximation
for i in range(2, terms + 1):
approximation -= x**i / i
# Compare the approximation with the exact value
exact_value = math.log(1.2)
error = abs(approximation - exact_value)
print("Approximation:", approximation)
print("Exact value:", exact_value)
print("Error:", error)
Numerical Comparisons
Table 1 compares the accuracy of the Taylor series approximation for ln(1 + x) with different numbers of terms:
| Number of Terms | x | Approximate Value | Error |
|---|---|---|---|
| 1 | 0.2 | 0.18 | 0.002 |
| 3 | 0.2 | 0.1826 | 0.0004 |
| 5 | 0.2 | 0.18265 | 0.00005 |
| 7 | 0.2 | 0.182645 | 0.000005 |
As the number of terms increases, the approximation becomes more accurate and the error decreases.
Convergence Analysis
The rate of convergence of the Taylor series for ln(1 + x) can be analyzed using a technique known as the remainder term estimate. The remainder term is the difference between the exact value of ln(1 + x) and the partial sum of the Taylor series.
The remainder term for the Taylor series of ln(1 + x) is given by:
R_n(x) = (-1)^n * (x^(n+1) / (n+1)) * (1/(1+c))
where c is some value between 0 and x.
The following inequality provides an upper bound for the remainder term:
|R_n(x)| <= |x^(n+1) / (n+1)| / 2
Using this inequality, we can determine the number of terms needed to achieve a desired level of accuracy.
Extension to Complex Numbers
The Taylor series expansion for ln(1 + x) can be extended to complex numbers using the concept of the complex logarithm. The complex logarithm, denoted as Ln(z), is defined as:
Ln(z) = ln(|z|) + i arg(z)
where |z| is the magnitude of z and arg(z) is its argument.
The Taylor series expansion for Ln(z) around z = 1 is given by:
Ln(z) = (z - 1) - (z - 1)²/2 + (z - 1)³/3 - (z - 1)⁴/4 + ...
where ... denotes higher-order terms. This series converges for |z - 1| < 1.
Comparison of Logarithmic Functions
Table 2 provides a comparison of the natural logarithm, common logarithm, and binary logarithm:
| Function | Base | Range |
|---|---|---|
| Natural logarithm (ln) | e ≈ 2.718 | (-∞, ∞) |
| Common logarithm (log) | 10 | (0, ∞) |
| Binary logarithm (log₂) | 2 | (0, ∞) |
The natural logarithm is the most commonly used logarithmic function, as it is related to the exponential function by the identity e^ln(x) = x. The common logarithm is often used in engineering and scientific applications, while the binary logarithm is widely employed in computer science and information theory.
New Application: Logarithmic Interpolation
Logarithmic interpolation is a novel technique that leverages the Taylor series expansion of ln(1 + x) to perform efficient interpolation of data. This approach involves taking the logarithm of the data points, applying interpolation to the transformed data, and then exponentiating the result to obtain the interpolated values.
Logarithmic interpolation offers several advantages over traditional interpolation methods, including:
- Enhanced accuracy: The logarithmic transformation can linearize nonlinear data, leading to more accurate interpolated values.
- Handling of negative and zero values: Logarithmic interpolation can handle negative and zero values, which is not possible with certain other interpolation methods.
- Computational efficiency: The Taylor series expansion provides a computationally efficient way to perform logarithmic interpolation.
Future Directions
The study of Taylor series expansions for logarithmic functions continues to be an active area of research. Some promising future directions include:
- Developing improved convergence acceleration techniques: Researchers are exploring novel approaches to accelerate the convergence of Taylor series for logarithmic functions, especially for large values of x.
- Investigating applications in machine learning: Taylor series expansions can be used for feature engineering and model training in machine learning algorithms.
- Extending to multivariate logarithmic functions: The Taylor series expansion can be extended to multivariate logarithmic functions, enabling the approximation of complex functions of multiple variables.
Frequently Asked Questions
1. What is the range of validity for the Taylor series expansion of ln(1 + x)?
The Taylor series expansion for ln(1 + x) is valid for |x| < 1.
2. How many terms are necessary to achieve a desired level of accuracy?
The number of terms needed depends on the desired accuracy and the value of x. The remainder term estimate can be used to determine the minimum number of terms required.
3. Can the Taylor series expansion be used to approximate the logarithm of negative numbers?
No, the Taylor series expansion for ln(1 + x) cannot be used to approximate the logarithm of negative numbers.
4. How does logarithmic interpolation compare to other interpolation methods?
Logarithmic interpolation offers enhanced accuracy, can handle negative and zero values, and is computationally efficient.
5. What are some potential applications of logarithmic interpolation?
Potential applications of logarithmic interpolation include data analysis, signal processing, and image processing.
6. What is the Taylor series expansion for ln(1 - x)?
The Taylor series expansion for ln(1 - x) is given by:
ln(1 - x) = -x - x²/2 - x³/3 - x⁴/4 - ...
where ... denotes higher-order terms. This series converges for |x| < 1.
7. What is the derivative of the natural logarithm?
The derivative of the natural logarithm is given by:
d/dx ln(x) = 1/x
8. What is the integral of the natural logarithm?
The integral of the natural logarithm is given by:
∫ ln(x) dx = x ln(x) - x + C
where C is the constant of integration.