Introduction
The t-test is a statistical test that compares the means of two independent groups. It is commonly used to determine if there is a significant difference between the means of two populations. The t-test is a powerful tool that can be used in a variety of applications, including:

- Comparing the effectiveness of two different treatments
- Determining if there is a significant difference between the means of two populations
- Testing hypotheses about the mean of a population
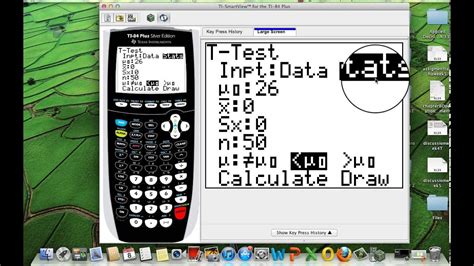
Performing a T-Test on TI-84
Performing a t-test on a TI-84 is relatively easy. The following steps will guide you through the process:
- Enter the data for the two groups into the TI-84.
- Press the “STAT” button and select “TESTS.”
- Select “T-Test” and then “2-SampTTest.”
- Enter the values for the following parameters:
- X1: The data for the first group
- X2: The data for the second group
- Hypothesized mean difference: The hypothesized difference between the means of the two groups
- Alternative hypothesis: The alternative hypothesis being tested
- Press “ENTER” to perform the t-test.
The TI-84 will display the results of the t-test, including the t-value, the degrees of freedom, and the p-value.
Interpreting the Results of a T-Test
The results of a t-test can be interpreted as follows:
- T-value: The t-value is a measure of the difference between the means of the two groups. A larger t-value indicates a greater difference between the means.
- Degrees of freedom: The degrees of freedom is the number of observations in the two groups minus 2.
- P-value: The p-value is the probability of obtaining a t-value as large as or larger than the one that was observed, assuming that there is no difference between the means of the two groups. A smaller p-value indicates that there is a smaller probability of obtaining a t-value as large as or larger than the one that was observed, and thus a greater likelihood that there is a difference between the means of the two groups.
If the p-value is less than the alpha level (typically 0.05), then the null hypothesis is rejected and the alternative hypothesis is accepted. This means that there is a statistically significant difference between the means of the two groups.
Common Mistakes to Avoid
When performing a t-test, it is important to avoid the following common mistakes:
- Using the wrong data: The data used in a t-test must be independent and normally distributed.
- Using the wrong alternative hypothesis: The alternative hypothesis must be consistent with the research question being asked.
- Not considering the effect size: The effect size is a measure of the magnitude of the difference between the means of the two groups. A small effect size may not be statistically significant, even if the p-value is less than the alpha level.
- Drawing the wrong conclusion: The results of a t-test should be interpreted in the context of the research question being asked. A statistically significant difference does not necessarily mean that the difference is practically significant.
Step-by-Step Approach
The following step-by-step approach can help you to avoid the common mistakes and ensure that you are performing a t-test correctly:
- Define the research question. What do you want to learn from the t-test?
- Select the appropriate data. The data must be independent and normally distributed.
- Choose the alternative hypothesis. The alternative hypothesis must be consistent with the research question being asked.
- Perform the t-test using the TI-84.
- Interpret the results. Consider the t-value, the degrees of freedom, the p-value, and the effect size.
- Draw a conclusion. The conclusion should be based on the results of the t-test and the context of the research question being asked.
Why T-Test Matters
The t-test is a powerful tool that can be used to determine if there is a statistically significant difference between the means of two independent groups. The t-test is commonly used in a variety of applications, including:
- Comparing the effectiveness of two different treatments
- Determining if there is a significant difference between the means of two populations
- Testing hypotheses about the mean of a population
The t-test is a valuable tool for researchers and practitioners alike. By understanding how to perform a t-test, you can use this powerful tool to answer a variety of research questions.
Benefits of Using T-Test
The t-test offers a number of benefits, including:
- Simplicity: The t-test is a relatively simple test to perform, even for those with limited statistical knowledge.
- Versatility: The t-test can be used to compare the means of two independent groups, regardless of the distribution of the data.
- Power: The t-test is a powerful test that can detect statistically significant differences, even when the effect size is small.
The t-test is a valuable tool that can be used in a variety of applications. By understanding the benefits of the t-test, you can use this powerful tool to answer a variety of research questions.
Appendix
Table 1: Critical Values for the t-Distribution
| Degrees of freedom | t-value (alpha = 0.05) |
|---|---|
| 1 | 12.706 |
| 2 | 4.303 |
| 3 | 3.182 |
| 4 | 2.776 |
| 5 | 2.571 |
| 6 | 2.447 |
| 7 | 2.365 |
| 8 | 2.306 |
| 9 | 2.262 |
| 10 | 2.228 |
Table 2: Effect Sizes for the t-Test
| Effect size | Cohen’s d |
|---|---|
| Small | 0.2 |
| Medium | 0.5 |
| Large | 0.8 |
Table 3: Common Mistakes to Avoid When Performing a T-Test
| Mistake | Description |
|---|---|
| Using the wrong data | The data used in a t-test must be independent and normally distributed. |
| Using the wrong alternative hypothesis | The alternative hypothesis must be consistent with the research question being asked. |
| Not considering the effect size | The effect size is a measure of the magnitude of the difference between the means of the two groups. A small effect size may not be statistically significant, even if the p-value is less than the alpha level. |
| Drawing the wrong conclusion | The results of a t-test should be interpreted in the context of the research question being asked. A statistically significant difference does not necessarily mean that the difference is practically significant. |
Table 4: Step-by-Step Approach to Performing a T-Test
| Step | Description |
|---|---|
| 1 | Define the research question. |
| 2 | Select the appropriate data. |
| 3 | Choose the alternative hypothesis. |
| 4 | Perform the t-test using the TI-84. |
| 5 | Interpret the results. |
| 6 | Draw a conclusion. |