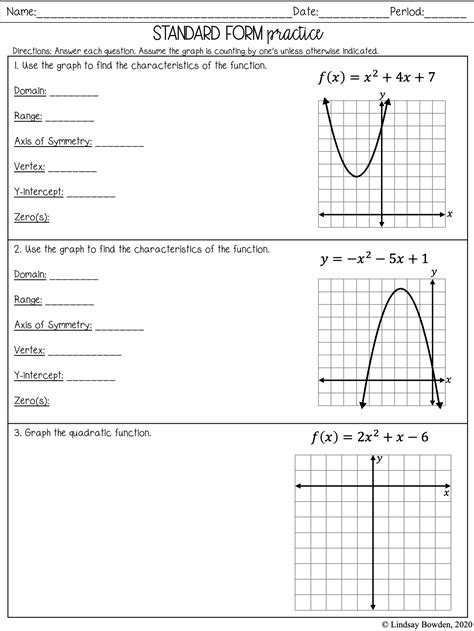
Mastering the art of solving and graphing quadratics is crucial for success in algebra and beyond. This online practice test is meticulously designed to provide you with a comprehensive and engaging experience, enabling you to refine your skills and excel in this essential mathematical concept.

Understanding Quadratics
Quadratics, also known as quadratic equations, are polynomial equations of the second degree. They take the general form of ax² + bx + c = 0, where ‘a’, ‘b’, and ‘c’ are real numbers and ‘a’ is non-zero. The graph of a quadratic equation is a parabola, which is a U-shaped curve that opens upward or downward.
Solving Quadratics
There are various methods for solving quadratics, including:
- Factoring: This method involves expressing the quadratic as a product of two linear factors. For example, x² – 4 = (x – 2)(x + 2).
- Completing the square: This method involves adding and subtracting the square of half the coefficient of x to both sides of the equation.
- Using the quadratic formula: This formula provides a general solution for any quadratic equation: x = (-b ± √(b² – 4ac)) / 2a.
Graphing Quadratics
To graph a quadratic, you can use the following steps:
- Find the vertex of the parabola using the formula: (-b/2a, f(-b/2a)).
- Plot the vertex and the two x-intercepts (if any) on the coordinate plane.
- Sketch the parabola through these points, ensuring that it opens upward or downward depending on the sign of ‘a’.
Benefits of Solving and Graphing Quadratics
Mastering these skills offers numerous benefits:
- Enhanced Mathematical Proficiency: Solving and graphing quadratics strengthens your algebraic and geometric understanding.
- Problem-Solving Skills: Quadratic equations are used to solve real-world problems in various fields, such as engineering, science, and finance.
- Improved Critical Thinking: Analyzing the graph of a quadratic allows you to make predictions and draw conclusions about its behavior.
- Academic Success: Quadratic functions are a cornerstone of higher-level mathematics, including calculus and trigonometry.
Online Practice Test
This online practice test comprises a series of interactive questions that cover key aspects of solving and graphing quadratics. Each question provides immediate feedback and detailed explanations, helping you identify areas for improvement and reinforce your understanding.
Common Mistakes to Avoid
To avoid common pitfalls, keep these tips in mind:
- Ensure the quadratic equation is in standard form before attempting to solve it.
- Check your factoring carefully for any errors, especially when dealing with negative coefficients.
- When completing the square, do not forget to subtract the constant term twice.
- When graphing, pay attention to the vertex and x-intercepts to determine the parabola’s orientation and shape.
Why Solving and Graphing Quadratics Matters
Quadratics play a vital role in various applications, including:
- Projectile Motion: The trajectory of a projectile can be modeled using a quadratic equation.
- Area and Volume: Optimizing the dimensions of rectangular objects, such as boxes, requires solving quadratic equations.
- Electrical Circuits: Analyzing the behavior of electrical circuits involves using quadratic functions to calculate current and voltage.
- Probability: Some probability distributions, such as the normal distribution, are based on quadratic functions.
Frequently Asked Questions
-
What is the vertex of a parabola?
The vertex is the point where the parabola changes direction. -
How do you find the x-intercepts of a quadratic?
Set y = 0 and solve the resulting equation for x. -
What is the discriminant of a quadratic?
The discriminant (b² – 4ac) determines the number and nature of the roots of the quadratic. -
How can I check my answers when graphing quadratics?
Use the vertex and x-intercepts to draw the parabola and compare it to the given equation. -
What are some tips for improving my skills in solving and graphing quadratics?
Practice regularly, use different methods, and seek help when needed. -
How are quadratics used in real-world applications?
They are used in various fields, including physics, engineering, economics, and biology. -
What are the limitations of using online practice tests?
They may not provide personalized feedback or address specific areas of difficulty. -
Can I improve my understanding of quadratics without practicing?
No, consistent practice is essential for developing proficiency.
Conclusion
Solving and graphing quadratics is a fundamental mathematical skill with far-reaching applications. By utilizing this online practice test, you can hone your abilities, build confidence, and prepare yourself for success in higher-level mathematics and beyond. Embrace the challenge, practice consistently, and experience the transformative benefits of mastering quadratics.