In the world of physics, understanding the motion of objects is crucial. Rotational inertia, a fundamental property of rotating objects, plays a pivotal role in determining their behavior. In this comprehensive guide, we delve into the intricacies of the rotational inertia of a rod, exploring its applications, calculations, and practical implications.

What is Rotational Inertia?
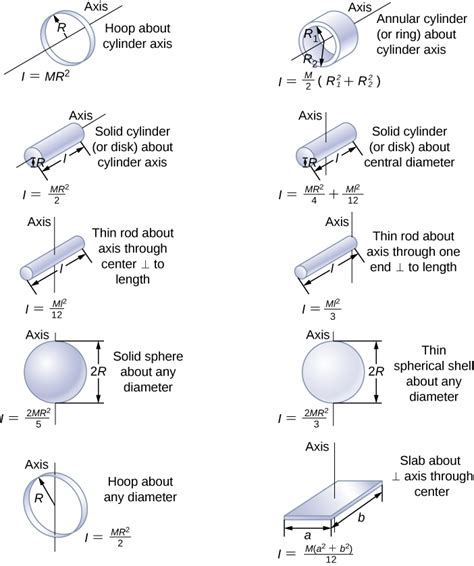
Rotational inertia, also known as moment of inertia, measures an object’s resistance to changes in its angular velocity. It is a scalar quantity that depends on the object’s mass, shape, and distribution of mass. For a rod rotating about its central axis, the rotational inertia is given by:
I = (1/12) * m * L^2
where:
- I is the rotational inertia
- m is the mass of the rod
- L is the length of the rod
Significance of Rotational Inertia
Rotational inertia is crucial in various applications, including:
- Engineering: Designing structures that withstand dynamic forces, such as bridges, turbines, and aircraft wings.
- Sports: Analyzing the dynamics of athletes’ movements, such as in gymnastics, golf, and ice skating.
- Machinery: Understanding the behavior of rotating components, such as gears, pulleys, and flywheels.
- Physics: Determining the period of oscillation of rotating systems, such as pendulums and torsion springs.
Applications of Rotational Inertia in Robotics
In robotics, understanding rotational inertia is essential for:
- Motion planning: Optimizing the trajectory of robotic arms to minimize energy consumption and improve accuracy.
- Actuator selection: Choosing actuators with appropriate torque and power to overcome the rotational inertia of robotic joints.
- Stability control: Designing control systems that maintain the stability of robots during dynamic movements.
Table 1: Rotational Inertia of Common Objects
| Object | Rotational Inertia (kg-m^2) |
|---|---|
| Thin rod (rotating about central axis) | (1/12) * m * L^2 |
| Solid cylinder (rotating about central axis) | (1/2) * m * R^2 |
| Hollow cylinder (rotating about central axis) | m * (R^2 – r^2) / 2 |
| Sphere (rotating about diameter) | (2/5) * m * R^2 |
Tips and Tricks
- To reduce the rotational inertia of a rotating system, distribute mass as far as possible from the axis of rotation.
- Use lightweight materials or hollow structures to minimize mass while maintaining structural integrity.
- Consider using flywheels to store rotational energy and compensate for variations in angular velocity.
- Incorporate damping mechanisms to reduce the effects of rotational inertia on system stability.
FAQs
-
What is the SI unit of rotational inertia?
– The SI unit of rotational inertia is kilogram-meter squared (kg-m^2). -
How does rotational inertia differ from mass?
– Mass measures an object’s resistance to acceleration, while rotational inertia measures its resistance to changes in angular velocity. -
Why is rotational inertia important in gyroscopes?
– Rotational inertia provides stability to gyroscopes, allowing them to maintain a constant angular velocity and orientation. -
How can I calculate the rotational inertia of an irregular object?
– Use the parallel axis theorem or integral calculus to determine the rotational inertia of an irregular object. -
What is the rotational inertia of a point mass?
– The rotational inertia of a point mass is zero. -
How does rotational inertia affect the angular acceleration of an object?
– Rotational inertia is inversely proportional to angular acceleration, meaning that objects with higher rotational inertia will have lower angular accelerations.
Conclusion
Understanding the rotational inertia of a rod is fundamental to analyzing the behavior of rotating objects in various applications. By leveraging the concepts and insights presented in this guide, engineers, scientists, and researchers can optimize the design and performance of systems involving rotational motion. As technology continues to advance, new and innovative applications for rotational inertia will undoubtedly emerge.