In the realm of statistics, the concepts of population proportion and sample proportion play pivotal roles. Understanding the difference between these two measures is crucial for accurate data interpretation and hypothesis testing.

Population Proportion
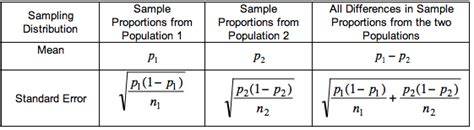
The population proportion, denoted by the Greek letter π, represents the proportion or percentage of a specific characteristic or attribute in a population. It is a parameter that describes the entire population. For instance, if 65% of a population is female, then the population proportion of females is 0.65.
Sample Proportion
On the other hand, a sample proportion, denoted by the Latin letter p, refers to the proportion or percentage of a specific characteristic or attribute in a sample. It is a statistic that estimates the population proportion based on a subset of the population. For example, if a sample of 100 individuals yields 60 females, then the sample proportion of females is 0.60.
Discrepancy between Population and Sample Proportions
Due to random sampling, the sample proportion will not always be exactly equal to the population proportion. This discrepancy arises because the sample represents a subset of the population and is subject to sampling error. The magnitude of the discrepancy depends on the sample size and the variability within the population.
Hypothesis Testing
The discrepancy between population and sample proportions becomes particularly important in hypothesis testing. Hypothesis testing involves comparing a sample proportion to a hypothesized population proportion to determine whether there is a statistically significant difference. If the discrepancy is large enough and unlikely to occur by chance alone, then the hypothesis can be rejected.
Confidence Intervals
Confidence intervals are another statistical tool that incorporates the discrepancy between population and sample proportions. A confidence interval provides a range of plausible values for the population proportion that is based on the sample proportion. The width of the confidence interval is determined by the sample size and the variability within the population.
Applications of Population and Sample Proportions
The concepts of population proportion and sample proportion have a wide range of applications in various fields, including:
- Medicine: Determining the prevalence of diseases or the effectiveness of treatments.
- Marketing: Estimating consumer preferences or market share.
- Education: Assessing student performance or evaluating the effectiveness of teaching methods.
- Politics: Predicting election outcomes or measuring public opinion.
- Innovation: Identifying untapped markets or developing new products and services.
Tips for Accurate Estimation
To ensure accurate estimation of population and sample proportions, consider the following tips:
- Use a representative sample: The sample should reflect the characteristics of the entire population.
- Increase the sample size: Larger sample sizes reduce sampling error and increase the accuracy of the estimate.
- Account for variability: The estimate should be adjusted based on the variability within the population.
Pros and Cons of Population and Sample Proportions
| Characteristic | Population Proportion | Sample Proportion |
|---|---|---|
| Accuracy | More accurate | Less accurate |
| Cost and time | More expensive and time-consuming | Less expensive and less time-consuming |
| Applicability | Can be generalized to the entire population | Can only be generalized to the sample |
| Sampling error | Not subject to sampling error | Subject to sampling error |
FAQs
1. What is the difference between a population proportion and a sample proportion?
A population proportion is a parameter that describes the entire population, while a sample proportion is a statistic that estimates the population proportion based on a subset of the population.
2. Why is there a discrepancy between population and sample proportions?
Sampling error causes the discrepancy between population and sample proportions.
3. How can we reduce the discrepancy between population and sample proportions?
Increasing the sample size and accounting for variability can reduce the discrepancy.
4. What are the applications of population and sample proportions?
Applications include medicine, marketing, education, politics, and innovation.
5. What are the pros and cons of population and sample proportions?
Pros: Population proportions are more accurate, while sample proportions are less expensive and less time-consuming. Cons: Population proportions can be more expensive and time-consuming to obtain, while sample proportions may not be generalizable to the entire population.
6. How can we ensure accurate estimation of population and sample proportions?
Use a representative sample, increase the sample size, and account for variability.