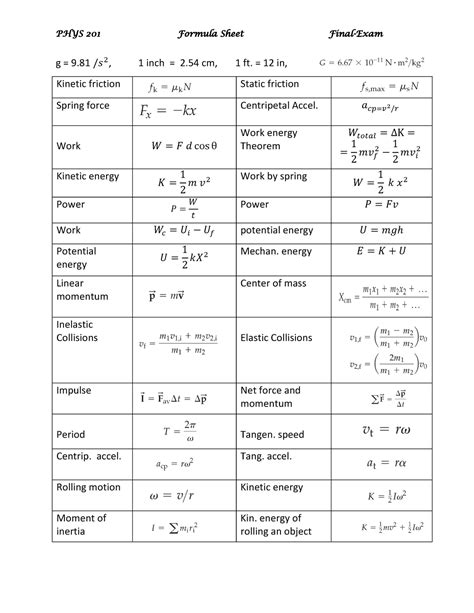
Mastering physics requires a strong foundation in core equations. This comprehensive equation sheet provides a convenient reference point for students navigating the complexities of Physics 1.

Kinematics
Constant Velocity Motion
- Displacement: Δx = v₀t + (1/2)at²
- Velocity: v = v₀ + at
- Acceleration: a = (v – v₀) / t
Variable Acceleration Motion
- Displacement: Δx = (v₀ + v)t / 2
- Velocity: v² = v₀² + 2aΔx
- Acceleration: a = (v² – v₀²) / 2Δx
Dynamics
Newton’s Second Law
- Force: F = ma
- Mass: m = F / a
Gravity
- Weight: W = mg
- Gravitational Force: F = Gm₁m₂ / r²
Momentum and Energy
Momentum
- Linear Momentum: p = mv
- Impulse: J = Ft
Energy
- Kinetic Energy: KE = (1/2)mv²
- Potential Energy: PE = mgh
- Conservation of Energy: ΔKE + ΔPE = 0
Rotational Motion
Angular Velocity and Displacement
- Angular Velocity: ω = Δθ / Δt
- Angular Displacement: Δθ = ωt
Moment of Inertia
- Moment of Inertia: I = mr²
Rotational Energy
- Rotational Kinetic Energy: KE = (1/2)Iω²
Waves
Wave Types
- Transverse Waves: Particles oscillate perpendicular to the wave direction
- Longitudinal Waves: Particles oscillate parallel to the wave direction
Wave Characteristics
- Wavelength: λ = c / f
- Frequency: f = c / λ
- Wave Speed: c = fλ
Useful Tables
Table 1: Physical Constants
| Constant | Value |
|---|---|
| Gravitational Constant (G) | 6.674 × 10⁻¹¹ m³ kg⁻¹ s⁻² |
| Speed of Light (c) | 2.998 × 10⁸ m/s |
| Planck’s Constant (h) | 6.626 × 10⁻³⁴ J s |
| Coulomb Constant (k) | 8.988 × 10⁹ N m² C⁻² |
Table 2: Kinematic Equations
| Equation | Use |
|---|---|
| Δx = v₀t + (1/2)at² | Constant velocity or uniform acceleration |
| v = v₀ + at | Constant acceleration |
| a = (v – v₀) / t | Calculating acceleration from velocity changes |
| Δx = (v₀ + v)t / 2 | Variable acceleration |
| v² = v₀² + 2aΔx | Relating velocity and displacement |
| a = (v² – v₀²) / 2Δx | Relating acceleration, velocity, and displacement |
Table 3: Dynamics Equations
| Equation | Use |
|---|---|
| F = ma | Calculating force from mass and acceleration |
| m = F / a | Calculating mass from force and acceleration |
| W = mg | Calculating weight from mass and gravity |
| F = Gm₁m₂ / r² | Calculating gravitational force between two masses |
Table 4: Energy Equations
| Equation | Use |
|---|---|
| KE = (1/2)mv² | Calculating kinetic energy from mass and velocity |
| PE = mgh | Calculating gravitational potential energy from mass, height, and gravity |
| ΔKE + ΔPE = 0 | Conservation of energy law |