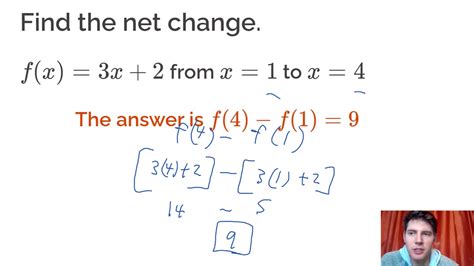Introduction

In the realm of mathematics, understanding the concept of net change is paramount for comprehending how variables transform over time. Whether it’s the velocity of a moving object or the interest accrued on an investment, grasping the essence of net change empowers us to unravel the intricate dance of change that shapes our world.
What is Net Change?
Net change refers to the overall alteration in the value of a variable between two distinct points in time or space. It is calculated by subtracting the initial value from the final value. Algebraically, net change can be expressed as:
Net Change = Final Value - Initial Value
Significance of Net Change
Net change plays a crucial role in various scientific and real-world applications. For instance, in physics, it allows us to determine the displacement of an object by subtracting its initial position from its final position. In economics, it helps us assess the growth or decline of an investment by comparing its starting value with its ending value.
Calculating Net Change
To calculate net change, follow these steps:
- Identify the Variable: Determine the variable whose change you need to determine.
- Establish Time or Space Points: Identify the two distinct points in time or space for which you want to calculate the change.
- Gather Values: Obtain the initial and final values of the variable at the specified points.
- Calculate Net Change: Subtract the initial value from the final value using the formula mentioned above.
Applications of Net Change
The concept of net change finds application in a myriad of fields, including:
- Physics: Calculating velocity, acceleration, and displacement
- Economics: Assessing investment growth, inflation, and consumer spending
- Chemistry: Determining the concentration change of reactants and products
- Biology: Analyzing population growth, cell division, and gene expression
- Environmental Science: Monitoring pollution levels, climate change, and resource depletion
Tables for Net Change
| Variable | Initial Value | Final Value | Net Change |
|---|---|---|---|
| Velocity | 10 m/s | 20 m/s | 10 m/s |
| Investment Value | $1,000 | $1,200 | $200 |
| Concentration | 0.5 M | 1.0 M | 0.5 M |
| Population | 100 individuals | 150 individuals | 50 individuals |
| Temperature | 20°C | 30°C | 10°C |
Tips and Tricks
- Always ensure that the units of the initial and final values are the same before calculating net change.
- For variables that can increase or decrease, specify whether the net change is positive (increase) or negative (decrease).
- When calculating net change over multiple time or space intervals, be mindful of the order of values.
Benefits of Understanding Net Change
Comprehending net change offers several benefits:
- Enhanced Problem-Solving Abilities: It enables you to solve complex problems involving changes in variables.
- Improved Data Interpretation: It assists in interpreting data sets that track changes over time.
- Informed Decision-Making: It empowers you to make informed decisions based on an understanding of how variables have changed.
Conclusion
Net change is a fundamental concept in algebra that provides insights into the evolution of variables. By understanding net change, we unlock the ability to analyze and quantify change, empowering us to make sense of the dynamic world around us. Its applications span a wide range of disciplines, from physics to economics, and its benefits extend far beyond the confines of the classroom.