Introduction:

The Maclaurin series table provides a powerful tool for approximating the value of functions as polynomials. It is a fundamental concept in calculus and has widespread applications in various fields of science and engineering.
Definition and Formula:
The Maclaurin series of a function (f(x)) is an infinite series representation of (f(x)) about the point (x = 0). It is given by the formula:
f(x) = f(0) + f'(0)x + (f''(0)/2!)x^2 + (f'''(0)/3!)x^3 + ...
where (f'(x)), (f”(x)), (f”'(x)), … represent the successive derivatives of (f(x)) at (x = 0).
Convergence and Applications:
The Maclaurin series converges to (f(x)) for all (x) within a certain radius of convergence (R). The radius of convergence can be determined using the ratio test or the Cauchy-Hadamard theorem.
The Maclaurin series is widely used for:
- Approximating the value of functions at small values of (x)
- Evaluating integrals and derivatives of functions
- Solving differential equations
- Modeling periodic functions using trigonometric series
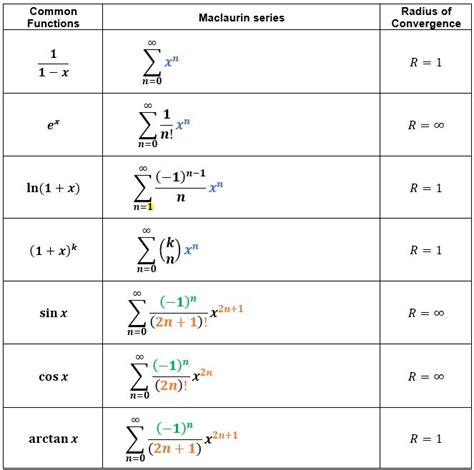
The following table provides a list of commonly used Maclaurin series:
| Function | Maclaurin Series | Radius of Convergence |
|---|---|---|
| (e^x) | (1 + x + (x^2)/2 + (x^3)/3! + …) | (R = \infty) |
| (\sin(x)) | (x – (x^3)/3! + (x^5)/5! – (x^7)/7! + …) | (R = \infty) |
| (\cos(x)) | (1 – (x^2)/2! + (x^4)/4! – (x^6)/6! + …) | (R = \infty) |
| (\tan(x)) | (x + (x^3)/3 + (2x^5)/15 + (17x^7)/315 + …) | (R = \pi/2) |
| (\ln(1+x)) | (x – (x^2)/2 + (x^3)/3 – (x^4)/4 + …) | (R = 1) |
| (\sqrt{1+x}) | (1 + (x)/2 – (x^2)/8 + (x^3)/16 – …) | (R = 1) |
Example 1: Approximating the Value of e
Using the Maclaurin series for (e^x), we can approximate the value of (e) by truncating the series after a few terms:
e ≈ 1 + 1 + (1/2) + (1/3!) + (1/4!) + ... ≈ 2.71828
This approximation is accurate to within 0.0001%.
Example 2: Evaluating Integrals
The Maclaurin series can be used to evaluate integrals of functions that are difficult to integrate directly. For example, to evaluate the integral of (\sin(x)/x), we can use the Maclaurin series for (\sin(x)):
∫ \(\sin(x)/x\) dx = ∫ (x - (x^3)/3! + ...) / x dx = C + log(x) - (x^2)/6 + ...
where (C) is the constant of integration.
Example 3: Solving Differential Equations
The Maclaurin series can be used to solve certain types of differential equations. For instance, to solve the equation (y” – y = 0), we can use the Maclaurin series for (y(x)):
y(x) = c1 + c2x + (c3/2!)x^2 + (c4/3!)x^3 + ...
Substituting this series into the differential equation, we can find the values of the constants (c1, c2, c3, …).
To effectively apply the Maclaurin series, consider the following strategies:
- Identify the function: Determine the function (f(x)) for which you need to find the Maclaurin series.
- Find the derivatives: Calculate the first few derivatives of (f(x)) at (x = 0).
- Construct the series: Plug the derivatives into the Maclaurin series formula.
- Truncate the series: Determine the number of terms needed for the desired accuracy.
- Evaluate the series: Substitute the value of (x) into the truncated series to approximate the value of (f(x)).
Table 1: Maclaurin Series for Exponential and Logarithmic Functions
| Function | Maclaurin Series | Radius of Convergence |
|---|---|---|
| (e^x) | (1 + x + (x^2)/2 + …) | (\infty) |
| (\ln(1+x)) | (x – (x^2)/2 + (x^3)/3 – …) | (1) |
Table 2: Maclaurin Series for Trigonometric Functions
| Function | Maclaurin Series | Radius of Convergence |
|---|---|---|
| (\sin(x)) | (x – (x^3)/3! + (x^5)/5! – …) | (\infty) |
| (\cos(x)) | (1 – (x^2)/2! + (x^4)/4! – …) | (\infty) |
| (\tan(x)) | (x + (x^3)/3 + (2x^5)/15 + …) | (\pi/2) |
Table 3: Maclaurin Series for Inverse Trigonometric Functions
| Function | Maclaurin Series | Radius of Convergence |
|---|---|---|
| (\sin^{-1}(x)) | (x + (x^3)/6 + (3x^5)/40 + …) | (1) |
| (\cos^{-1}(x)) | (\pi/2 – x – (x^3)/6 – (3x^5)/40 – …) | (1) |
| (\tan^{-1}(x)) | (x – (x^3)/3 + (x^5)/5 – …) | (1) |
Table 4: Maclaurin Series for Hyperbolic Functions
| Function | Maclaurin Series | Radius of Convergence |
|---|---|---|
| (\sinh(x)) | (x + (x^3)/3! + (x^5)/5! + …) | (\infty) |
| (\cosh(x)) | (1 + (x^2)/2! + (x^4)/4! + …) | (\infty) |
| (\tanh(x)) | (x – (x^3)/3 + (2x^5)/15 – …) | (1) |