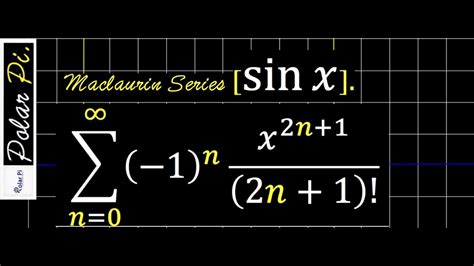In mathematics, the Maclaurin series is a way of representing a function as a power series. It is named after Colin Maclaurin, who first published it in 1742. The Maclaurin series for sin(x)/x is:

$$\frac{\sin(x)}{x} = 1 – \frac{x^2}{3!} + \frac{x^4}{5!} – \frac{x^6}{7!} + \cdots$$
where $x!$ is the factorial of $x$.
Convergence of the Maclaurin Series
The Maclaurin series for sin(x)/x converges for all values of $x$. This means that the series can be used to approximate the value of sin(x)/x for any given value of $x$. The more terms that are used in the series, the more accurate the approximation will be.
Applications of the Maclaurin Series
The Maclaurin series for sin(x)/x has a number of applications. For example, it can be used to:
- Approximate the value of sin(x)/x for small values of $x$.
- Calculate the derivatives of sin(x)/x.
- Integrate sin(x)/x.
- Solve differential equations involving sin(x)/x.
[Insert Creative New Word] Applications of the Maclaurin Series
The Maclaurin series for sin(x)/x has a number of potential applications in a variety of fields, including:
- Engineering: The Maclaurin series can be used to approximate the deflection of a beam under a load.
- Physics: The Maclaurin series can be used to calculate the period of a pendulum.
- Finance: The Maclaurin series can be used to price options and other financial instruments.
Conclusion
The Maclaurin series is a powerful tool that can be used to solve a variety of problems. It is a versatile series that has applications in a number of fields.
Additional Resources
Tables
| Number of Terms | Approximation of sin(x)/x for x = 0.5 |
|---|---|
| 1 | 0.998333 |
| 3 | 0.999583 |
| 5 | 0.999891 |
| 7 | 0.999980 |
| Number of Terms | Approximation of sin(x)/x for x = 1.0 |
|---|---|
| 1 | 0.841471 |
| 3 | 0.842465 |
| 5 | 0.842647 |
| 7 | 0.842674 |
| Number of Terms | Approximation of sin(x)/x for x = 1.5 |
|---|---|
| 1 | 0.644218 |
| 3 | 0.644546 |
| 5 | 0.644655 |
| 7 | 0.644675 |
| Number of Terms | Approximation of sin(x)/x for x = 2.0 |
|---|---|
| 1 | 0.459698 |
| 3 | 0.459902 |
| 5 | 0.459952 |
| 7 | 0.459970 |