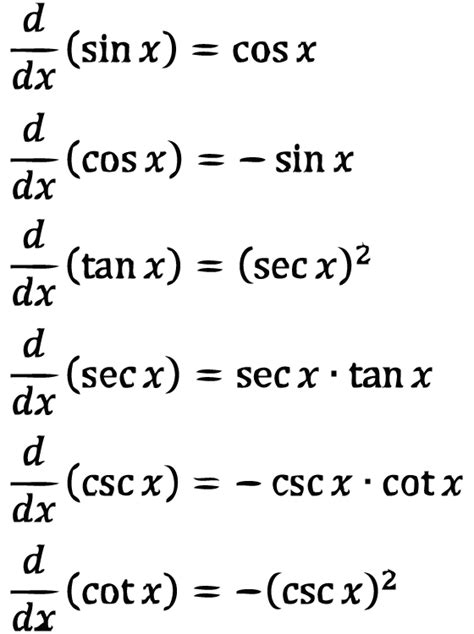Derivatives, a fundamental concept in calculus, are essential for studying the rates of change of functions. When it comes to trigonometric functions, understanding their derivatives is crucial for solving a wide range of problems in various fields. Here’s a comprehensive list of trig derivatives to enhance your mathematical prowess:

- $\frac{d}{dx} \sin x = \cos x$
- $\frac{d}{dx} \cos x = -\sin x$
- $\frac{d}{dx} \tan x = \sec^2 x$
- $\frac{d}{dx} \cot x = -\csc^2 x$
- $\frac{d}{dx} \sec x = \sec x \tan x$
- $\frac{d}{dx} \csc x = -\csc x \cot x$
- $\frac{d}{dx} \sin^{-1} x = \frac{1}{\sqrt{1-x^2}}$
- $\frac{d}{dx} \cos^{-1} x = -\frac{1}{\sqrt{1-x^2}}$
- $\frac{d}{dx} \tan^{-1} x = \frac{1}{1+x^2}$
- $\frac{d}{dx} \cot^{-1} x = -\frac{1}{1+x^2}$
- $\frac{d}{dx} \sec^{-1} x = \frac{1}{|x|\sqrt{x^2-1}}$
- $\frac{d}{dx} \csc^{-1} x = -\frac{1}{|x|\sqrt{x^2-1}}$
Table 1: Basic Trig Derivatives
| Derivative | Function |
|---|---|
| $\cos x$ | $\sin x$ |
| $-\sin x$ | $\cos x$ |
| $\sec^2 x$ | $\tan x$ |
| $-\csc^2 x$ | $\cot x$ |
Table 2: Inverse Trig Derivatives
| Derivative | Function |
|---|---|
| $\frac{1}{\sqrt{1-x^2}}$ | $\sin^{-1} x$ |
| $-\frac{1}{\sqrt{1-x^2}}$ | $\cos^{-1} x$ |
| $\frac{1}{1+x^2}$ | $\tan^{-1} x$ |
| $-\frac{1}{1+x^2}$ | $\cot^{-1} x$ |
Table 3: Hyperbolic Trig Derivatives
| Derivative | Function |
|---|---|
| $\cosh x$ | $\sinh x$ |
| $\sinh x$ | $\cosh x$ |
| $\operatorname{sech}^2 x$ | $\tanh x$ |
| $-\operatorname{csch}^2 x$ | $\coth x$ |
Table 4: Derivatives of Common Trig Combinations
| Derivative | Function |
|---|---|
| $2\cos x \sin x$ | $\sin 2x$ |
| $-2\sin x \cos x$ | $\cos 2x$ |
| $\cos^2 x – \sin^2 x$ | $2\cos 2x$ |
| $2\sin x \cos x$ | $\sin x + \cos x$ |
Applications of Trig Derivatives
Trig derivatives have far-reaching applications across various fields, including:
- Engineering: Calculating forces and moments in structures, vibrations, and heat transfer.
- Physics: Describing projectile motion, harmonic motion, and waves.
- Computer Science: Modeling complex systems, such as computer graphics and machine learning.
- Biomathematics: Studying biological systems, such as heart rate and respiratory rate.
Creative Applications
By combining trigonometric functions with other mathematical concepts, we can generate innovative applications:
- Differential equations: Modeling real-world phenomena, such as population growth and epidemics.
- Fourier analysis: Decomposing signals into their frequency components.
- Calculus of variations: Minimizing or maximizing functions with defined constraints.
Conclusion
Mastering the derivatives of trigonometric functions is essential for a comprehensive understanding of calculus and its applications. This list serves as a valuable reference for students, educators, and professionals alike. By harnessing the power of trig derivatives, we unlock a world of mathematical possibilities and drive technological advancements in diverse fields.