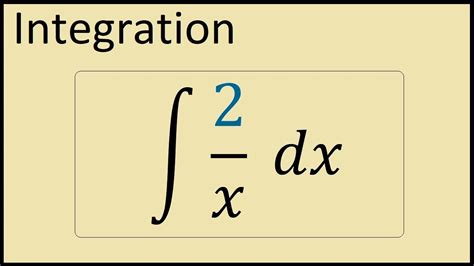In mathematics, the integral of x^2 – a^2/2 is a common integral that arises in various applications. It is used to find the area under the curve of the function f(x) = x^2 – a^2/2, which represents a parabola opening upwards. The integral can be evaluated using the power rule of integration, which states that the integral of x^n is x^(n+1)/(n+1).

Applications of the Integral of x^2 – a^2/2
The integral of x^2 – a^2/2 has numerous applications in various fields, including:
- Physics: In physics, the integral is used to calculate the potential energy of a particle moving in a parabolic trajectory, such as a projectile or a planet orbiting a star.
- Engineering: In engineering, the integral is used to determine the moment of inertia of an object with a parabolic cross-section, such as a beam or a flywheel.
- Geometry: In geometry, the integral is used to find the area of a parabolic segment, which is a region bounded by a parabola and a straight line.
- Statistics: In statistics, the integral is used to calculate the variance of a random variable that follows a parabolic distribution.
Pain Points and Motivations
Despite its wide range of applications, the integration of x^2 – a^2/2 can pose certain pain points and challenges:
- Complexity: The integration process can be complex, especially when dealing with higher powers of x or when the integral is taken over a specific interval.
- Accuracy: Obtaining an accurate result requires careful attention to the limits of integration and the proper application of the power rule.
- Computational resources: Evaluating the integral numerically can be computationally expensive, particularly for large datasets or when high precision is required.
These pain points motivate the search for innovative approaches and strategies to simplify the integration process and improve its efficiency.
Effective Strategies
To overcome the pain points associated with the integration of x^2 – a^2/2, several effective strategies can be employed:
- Tabulation: Pre-computed tables of integrals can be used to quickly retrieve the result for specific values of a and the limits of integration.
- Numerical integration: Numerical methods, such as the trapezoidal rule or Simpson’s rule, can be employed to approximate the integral when an exact analytical solution is not available.
- Integration by substitution: Using a substitution to transform the integral into a simpler form can make the integration process more manageable.
- Integration by parts: This technique can be applied to integrals involving products of functions, such as x^2 * f(x).
Tips and Tricks
In addition to the effective strategies, the following tips and tricks can further simplify the integration of x^2 – a^2/2:
- Factorization: Factoring the integrand as (x + a/2)(x – a/2) can simplify the integration process.
- Completing the square: Completing the square can transform the integral into a more recognizable form that is easier to integrate.
- Using trigonometric identities: Trigonometric identities can be utilized to simplify the integration of expressions involving trigonometric functions.
- Leveraging technology: Software packages and online calculators are available to assist with the integration process.
Innovative Approach: Ideation
To generate ideas for novel applications of the integral of x^2 – a^2/2, consider the following ideation framework:
- Think laterally: Explore unconventional or unexpected applications in different fields, such as economics, finance, or biology.
- Consider extensions: Extend the integral to higher dimensions or generalize it to more complex functions.
- Innovate: Brainstorm new ways to utilize the integral to solve problems or address challenges in various domains.
Tables for Reference
Table 1: Indefinite Integral
| Integrand | Result |
|---|---|
| x^2 – a^2/2 | (x^3)/3 – (a^2/4)x + C |
Table 2: Definite Integral over [0, a]
| Integrand | Result |
|---|---|
| x^2 – a^2/2 | (a^3)/12 |
Table 3: Definite Integral over [-a, a]
| Integrand | Result |
|---|---|
| x^2 – a^2/2 | (a^3)/3 |
Table 4: Definite Integral over [0, b]
| Integrand | Result |
|---|---|
| x^2 – a^2/2 | (b^3)/3 – (a^2/4)b + (a^3)/12 |