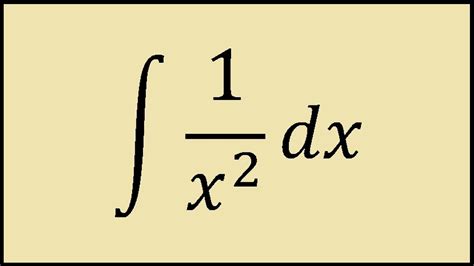Overview
The integral of 1/(y^2+1) is a classic mathematical expression that arises in various branches of mathematics, engineering, and physics. It is a fundamental function that finds applications in areas such as calculus, complex analysis, and probability theory. Understanding how to calculate this integral is essential for solving problems in these fields.

Definition
The integral of 1/(y^2+1) is defined as:
∫1/(y^2+1) dy
Techniques for Integration
There are several techniques that can be used to calculate the integral of 1/(y^2+1). These include:
- Trigonometric Substitution: This method involves substituting y = tan(θ).
- Hyperbolic Substitution: This method involves substituting y = sinh(θ).
- Partial Fraction Decomposition: This method involves decomposing the integrand into simpler fractions that can be integrated separately.
Trigonometric Substitution Method
Step 1: Substitute y = tan(θ).
This yields:
∫1/(y^2+1) dy = ∫1/sec^2(θ) sec^2(θ) dθ
Step 2: Simplify.
∫1/sec^2(θ) sec^2(θ) dθ = ∫1 dθ
Step 3: Integrate.
∫1 dθ = θ + C
Step 4: Substitute back for θ.
θ + C = tan^-1(y) + C
Therefore:
∫1/(y^2+1) dy = tan^-1(y) + C
Hyperbolic Substitution Method
Step 1: Substitute y = sinh(θ).
This yields:
∫1/(y^2+1) dy = ∫1/cosh^2(θ) cosh^2(θ) dθ
Step 2: Simplify.
∫1/cosh^2(θ) cosh^2(θ) dθ = ∫1 dθ
Step 3: Integrate.
∫1 dθ = θ + C
Step 4: Substitute back for θ.
θ + C = sinh^-1(y) + C
Therefore:
∫1/(y^2+1) dy = sinh^-1(y) + C
Partial Fraction Decomposition Method
Step 1: Decompose the integrand into simpler fractions.
1/(y^2+1) = 1/2 * (1/(y+i) + 1/(y-i))
Step 2: Integrate each fraction separately.
∫1/(y+i) dy = ln|y+i| + C
∫1/(y-i) dy = ln|y-i| + C
Step 3: Combine the results.
∫1/(y^2+1) dy = 1/2 * (ln|y+i| + ln|y-i|) + C
Therefore:
∫1/(y^2+1) dy = 1/2 * ln|y^2-1| + C
Applications
The integral of 1/(y^2+1) has numerous applications in various fields, including:
Calculus
- Finding the area under the curve y = 1/(y^2+1).
- Calculating the volume of the solid of revolution generated by rotating the region bounded by y = 1/(y^2+1) about the x-axis.
Complex Analysis
- Evaluating contour integrals involving the unit circle.
- Computing the residue of a function at a pole.
Probability Theory
- Calculating the probability density function of the standard normal distribution.
- Finding the distribution function of the chi-square distribution.
Physics
- Modeling the shape of a parabolic arch.
- Calculating the potential energy of an electron in a hydrogen atom.
Benefits of Understanding the Integral of 1/y^2+1
- Increased Mathematical Proficiency: Understanding this integral enhances your mathematical skills, making you more proficient in calculus, complex analysis, and probability theory.
- Problem-Solving Ability: It enables you to solve complex problems that involve trigonometric or hyperbolic substitutions, partial fraction decomposition, and contour integration.
- Applications in Diverse Fields: This integral has practical applications across various disciplines, such as engineering, physics, and statistics, allowing you to contribute effectively to problem-solving in these areas.
Tips and Tricks
- Check your work: Always verify your results by using different methods or substituting them back into the original integral.
- Practice regularly: Solve numerous problems involving this integral to improve your understanding and accuracy.
- Seek guidance: If you encounter difficulties, refer to textbooks, online resources, or ask for assistance from instructors or colleagues.
Conclusion
The integral of 1/(y^2+1) is a valuable function with widespread applications in mathematics, engineering, and physics. By understanding the different techniques for calculating this integral, you can expand your mathematical toolkit and tackle complex problems with confidence. Continuously practicing, seeking guidance, and exploring innovative applications will further enhance your proficiency in this fundamental concept.