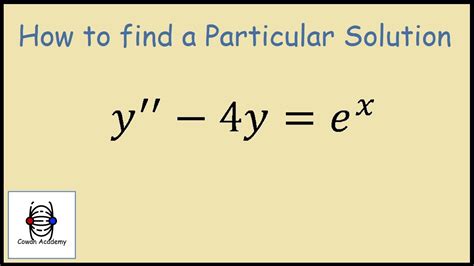In mathematics, a differential equation is an equation that contains derivatives of one or more unknown functions. Particular solutions are specific solutions to differential equations that satisfy given initial or boundary conditions.

Methods for Finding Particular Solutions
There are several methods for finding particular solutions to differential equations, including:
Method of Undetermined Coefficients
This method involves guessing a particular solution based on the form of the non-homogeneous term on the right-hand side of the differential equation. The coefficients of the guessed solution are then determined by solving a system of algebraic equations.
Method of Variation of Parameters
This method involves introducing new functions as parameters into the particular solution and then solving for the parameters by substituting the particular solution into the differential equation.
Method of Integrating Factors
This method involves multiplying the differential equation by a function (called an integrating factor) that makes the equation integrable. The equation can then be solved by integrating both sides.
Using Software
There are also software packages available that can solve differential equations numerically and find particular solutions.
Applications of Particular Solutions
Particular solutions to differential equations are used in a wide variety of applications, including:
- Modeling physical phenomena, such as the motion of a projectile or the flow of fluid
- Designing engineering systems, such as bridges or aircraft
- Predicting the behavior of biological systems, such as the spread of a disease
Step-by-Step Approach
The following is a step-by-step approach to finding a particular solution to a differential equation:
- Identify the type of differential equation. Determine whether the equation is ordinary or partial, linear or nonlinear, and homogeneous or non-homogeneous.
- Choose a method for finding the particular solution. The most appropriate method will depend on the type of differential equation.
- Solve for the unknown function. Use the chosen method to determine the particular solution that satisfies the given initial or boundary conditions.
- Check your solution. Substitute the particular solution back into the differential equation to verify that it satisfies the equation.
Tips and Tricks
- When guessing a particular solution using the method of undetermined coefficients, it is often helpful to use the form of the non-homogeneous term. For example, if the non-homogeneous term is a polynomial, guess a particular solution that is also a polynomial of the same degree.
- The method of variation of parameters can be used to find particular solutions to non-homogeneous equations even when the non-homogeneous term is not a polynomial.
- Integrating factors can be used to solve linear differential equations that are not in the standard form.
- Software packages can be a valuable tool for solving differential equations numerically. However, it is important to understand the underlying methods used by the software in order to interpret the results correctly.
Common Mistakes to Avoid
- Not checking the solution. It is important to substitute the particular solution back into the differential equation to verify that it satisfies the equation.
- Using the incorrect method. The most appropriate method for finding a particular solution will depend on the type of differential equation.
- Making algebraic errors. It is important to pay careful attention to algebraic manipulations when solving differential equations.
- Not considering the initial or boundary conditions. The particular solution must satisfy the given initial or boundary conditions.
Tables
Table 1: Methods for Finding Particular Solutions
| Method | Type of Differential Equation | Suitable for |
|---|---|---|
| Method of Undetermined Coefficients | Non-homogeneous, linear | Non-homogeneous term has a simple form |
| Method of Variation of Parameters | Non-homogeneous, linear | Non-homogeneous term is not a polynomial |
| Method of Integrating Factors | Linear | Standard form |
Table 2: Applications of Particular Solutions
| Application | Area |
|—|—|—|
| Modeling physical phenomena | Physics, engineering |
| Designing engineering systems | Civil engineering, mechanical engineering |
| Predicting the behavior of biological systems | Biology, medicine |
Table 3: Tips and Tricks
| Tip | Trick |
|—|—|—|
| Guessing a particular solution | Use the form of the non-homogeneous term |
| Using the method of variation of parameters | Can solve for particular solutions even when the non-homogeneous term is not a polynomial |
| Using integrating factors | Can solve linear differential equations that are not in the standard form |
Table 4: Common Mistakes to Avoid
| Mistake | How to avoid |
|—|—|—|
| Not checking the solution | Substitute the particular solution back into the differential equation |
| Using the incorrect method | Choose the most appropriate method based on the type of differential equation |
| Making algebraic errors | Pay careful attention to algebraic manipulations |
| Not considering the initial or boundary conditions | The particular solution must satisfy the given initial or boundary conditions |