Hospital Rule Calculator: A Comprehensive Guide to Determining Limits of Indeterminate Forms
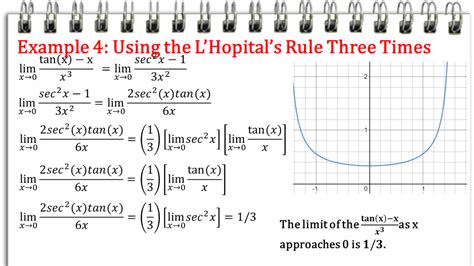
What is the Hospital Rule Calculator?
The hospital rule calculator is a tool designed to simplify the process of evaluating limits of indeterminate forms, which arise when applying basic limit laws results in an indeterminate expression (e.g., $\frac{0}{0}$ or $\frac{\infty}{\infty}$). It utilizes the L’Hôpital’s rule, a mathematical theorem that provides a systematic approach to solve such limits by taking derivatives.
How to Use the Hospital Rule Calculator
- Enter Expressions: Input the numerator and denominator of the expression you need to evaluate.
- Select L’Hôpital’s Rule: Choose “L’Hôpital’s Rule” as the method to evaluate the limit.
- Specify Derivatives: Indicate the number of times to apply the derivative.
- Evaluate: Click on “Evaluate” to obtain the limit.
Importance of the Hospital Rule
The hospital rule is a crucial tool in calculus as it:
- Evaluates Indeterminate Forms: Resolves limits that cannot be directly evaluated using standard limit laws.
- Enhances Calculus Accuracy: Provides a systematic and reliable approach to finding limits, leading to more precise results.
- Simplifies Complex Expressions: Often allows for the simplification of complex expressions, resulting in manageable limits.
Benefits of Using the Hospital Rule Calculator
- Time-Saving: Automates the tedious process of taking derivatives and evaluating limits, saving time and effort.
- Accuracy Guarantee: Ensures the accuracy of limit evaluations, reducing the risk of errors.
- Educational Aid: Helps students and researchers understand the concept and application of L’Hôpital’s rule.
- Analytical Toolkit: Serves as an analytical tool for finding limits in various mathematical and scientific fields.
Common Mistakes to Avoid
- Apply before Checking: Ensure that the expression results in an indeterminate form before applying L’Hôpital’s rule.
- Neglecting Derivatives: Remember to apply the derivative as many times as necessary to obtain a non-indeterminate form.
- Ignoring Assumptions: Be aware of the assumptions of L’Hôpital’s rule and verify that they are met.
Table of Indeterminate Forms and Hospital Rule Formulae
| Indeterminate Form | Hospital Rule Formula |
|---|---|
| $\frac{0}{0}$ | $\lim\limits_{x\to a}\frac{f(x)}{g(x)}=\lim\limits_{x\to a}\frac{f'(x)}{g'(x)}$ |
| $\frac{\infty}{\infty}$ | $\lim\limits_{x\to a}\frac{f(x)}{g(x)}=\lim\limits_{x\to a}\frac{f'(x)}{g'(x)}$ |
| $0\cdot\infty$ | $\lim\limits_{x\to a}f(x)g(x)=\lim\limits_{x\to a}\frac{f(x)}{1/g(x)}$ if $a\to\infty$ or $-\infty$ |
| $1^\infty$ | $\lim\limits_{x\to a}f(x)^{g(x)}=e^{\lim\limits_{x\to a}g(x)\ln f(x)}$ |
Applications of Hospital Rule Calculator
1. Integral Evaluation: Evaluating integrals that involve indeterminate forms after applying integration techniques.
2. Asymptotic Behavior: Determining the asymptotic behavior of functions by finding limits at infinity.
3. Convergence Tests: Using limits to test the convergence or divergence of infinite series.
4. Calculus Applications: Applying the hospital rule in advanced calculus topics such as differential equations and vector analysis.
FAQs
1. What happens if the limit still results in an indeterminate form after applying L’Hôpital’s rule?
– Apply L’Hôpital’s rule again or use alternative methods, such as Taylor series expansion.
2. Does the hospital rule calculator handle all cases of indeterminate forms?
– Yes, it evaluates all three common indeterminate forms: $\frac{0}{0}$, $\frac{\infty}{\infty}$, and $0\cdot\infty$.
3. Are there any limitations to using the hospital rule?
– It can become computationally complex when taking multiple derivatives, and it may not converge in certain cases.
4. What is a creative application of the hospital rule calculator?
– Solving differential equations by converting them into limits.
5. How does the hospital rule calculator benefit students?
– Simplifies the evaluation of limits, allowing them to focus on understanding the concepts.
6. What are the assumptions of L’Hôpital’s rule?
– The functions must be continuous and differentiable at the point of evaluation.
7. How does the hospital rule relate to numerical analysis?
– It forms the basis for numerical methods to approximate limits, such as Newton’s method.
8. What are some real-world examples of applying the hospital rule?
– Calculating the rate of growth of a population over time (limit of a difference quotient)
– Determining the acceleration of a body at a specific time (limit of a velocity-time graph)
