Introduction
In the realm of physics, understanding the relationship between gravitational force and the weight of objects is paramount. The gravitational force, denoted by the letter ‘g’, is the force of attraction between two objects with mass. This force plays a pivotal role in determining the weight of an object, a concept that is often misunderstood and conflated with mass.

Gravitational Force vs. Weight
Gravitational force, measured in newtons (N), is the result of the interaction between the masses of two objects. It is directly proportional to the product of the masses of the objects and inversely proportional to the square of the distance between them. The formula for gravitational force is given by:
F_g = G * (m1 * m2) / r^2
where:
- F_g is the gravitational force in newtons (N)
- G is the universal gravitational constant, equal to 6.674×10^-11 m³ kg^-1 s^-2
- m1 and m2 are the masses of the two objects in kilograms (kg)
- r is the distance between the centers of the two objects in meters (m)
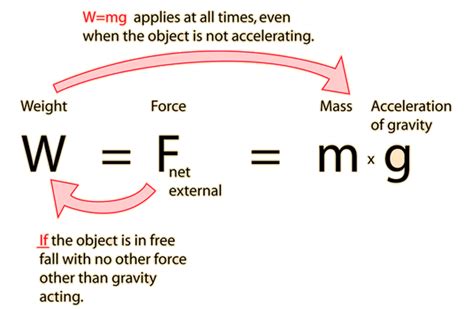
Weight, on the other hand, is the force exerted on an object due to the gravitational pull of a larger body, typically a planet like Earth. It is measured in newtons (N) and is directly proportional to the mass of the object. The formula for weight is given by:
W = m * g
where:
- W is the weight of the object in newtons (N)
- m is the mass of the object in kilograms (kg)
- g is the acceleration due to gravity, approximately 9.81 m/s² on Earth
The Role of Gravitational Force in Newton’s Second Law
Newton’s second law of motion states that the acceleration of an object is directly proportional to the net force acting on the object and inversely proportional to its mass. When an object is subjected to only the gravitational force of the Earth, Newton’s second law can be expressed as:
F_g = m * a
where:
- F_g is the gravitational force in newtons (N)
- m is the mass of the object in kilograms (kg)
- a is the acceleration due to gravity, approximately 9.81 m/s² on Earth
This relationship highlights the direct proportionality between gravitational force and the acceleration of an object due to gravity.
Newton and Pound: A Historical Perspective
The concept of gravitational force and its relationship to weight has been a topic of scientific inquiry for centuries. One of the most notable figures in this field is Sir Isaac Newton, who formulated the laws of motion and universal gravitation.
In 1687, Newton published his groundbreaking work, “Philosophiæ Naturalis Principia Mathematica,” which established the foundation for classical mechanics. In this work, he introduced the concept of gravitational force and the inverse square law, revolutionizing our understanding of the cosmos.
Another notable figure in this field is James Pound, an English astronomer and mathematician. In 1740, Pound conducted an experiment using a pendulum to demonstrate the variation in gravitational force with altitude. His findings supported Newton’s theory of universal gravitation.
Conversion of Gravitational Force to Newtons
To convert gravitational force from newtons (N) to pounds (lbs), the following equation can be used:
F_lbs = F_N * 0.2248
where:
- F_lbs is the gravitational force in pounds (lbs)
- F_N is the gravitational force in newtons (N)
For example, a gravitational force of 10 newtons is approximately equal to 2.248 pounds.
Applications of Gravitational Force in Engineering
The understanding of gravitational force is essential in various engineering fields, including:
- Structural engineering: Gravitational force plays a crucial role in the design and construction of bridges, buildings, and other structures to ensure their stability and prevent collapse.
- Aerospace engineering: Gravitational force is a primary consideration in designing aircraft and spacecraft, as it affects their trajectory, flight path, and fuel consumption.
- Geophysics: Gravitational force is used in geophysical surveys to study the Earth’s structure, composition, and density variations.
Innovative Applications of Gravitational Force
Beyond traditional engineering applications, the concept of gravitational force has also inspired innovative applications in other fields:
- Nanotechnology: Gravitational force can be harnessed to manipulate and assemble nanoscale materials, such as carbon nanotubes and graphene, with precision.
- Energy harvesting: Gravitational force can be used to generate electricity through devices that convert the potential energy stored in a raised mass into electrical energy.
- Biomechanics: Gravitational force plays a significant role in human and animal biomechanics, affecting posture, movement, and athletic performance.
Useful Tables
The following tables provide useful information related to gravitational force and its conversion to newtons:
| Mass (kg) | Weight on Earth (N) |
|---|---|
| 1 | 9.81 |
| 10 | 98.1 |
| 50 | 490.5 |
| 100 | 981 |
| Gravitational Force (N) | Equivalent Weight (lbs) |
|---|---|
| 1 | 0.2248 |
| 10 | 2.248 |
| 50 | 11.24 |
| 100 | 22.48 |
| Planet | Acceleration Due to Gravity (m/s²) |
|---|---|
| Earth | 9.81 |
| Mars | 3.71 |
| Jupiter | 24.79 |
| Saturn | 10.44 |
| Object | Mass (kg) | Weight on Earth (N) |
|---|---|---|
| Human | 75 | 735.75 |
| Car | 1000 | 9810 |
| Space Shuttle | 1000000 | 9810000 |
Tips and Tricks
- To estimate the gravitational force between two objects, use the following approximation:
F_g ≈ (m1 * m2) / r^2
where:
- m1 and m2 are the masses of the two objects in kilograms (kg)
-
r is the distance between the centers of the two objects in meters (m)
-
The acceleration due to gravity on Earth varies slightly with altitude and latitude. The standard value used for calculations is 9.81 m/s².
- When converting gravitational force to pounds, remember that 1 newton is approximately equal to 0.2248 pounds.
Common Mistakes to Avoid
- Do not confuse gravitational force with weight. Gravitational force is the force of attraction between two objects with mass, while weight is the force exerted on an object due to gravity.
- Do not assume that the acceleration due to gravity is always 9.81 m/s². It varies with altitude and latitude.
- Do not make approximations in the calculation of gravitational force without considering the accuracy requirements of the application.
Step-by-Step Approach to Convert Gravitational Force to Newtons
- Determine the masses: Determine the masses of the two objects involved in newtons (m1 and m2).
- Measure the distance: Measure the distance between the centers of the two objects in meters (r).
- Calculate the gravitational force: Use the formula
F_g = G * (m1 * m2) / r^2
to calculate the gravitational force in newtons.
Conclusion
Understanding the relationship between gravitational force and weight is fundamental to comprehending the interactions between objects and their environment. The conversion between gravitational force and newtons is essential in various scientific and engineering applications. By applying the principles and formulas discussed in this article, one can accurately calculate and interpret the gravitational force acting on objects, leading to advancements in fields ranging from structural engineering to nanotechnology.