Introduction

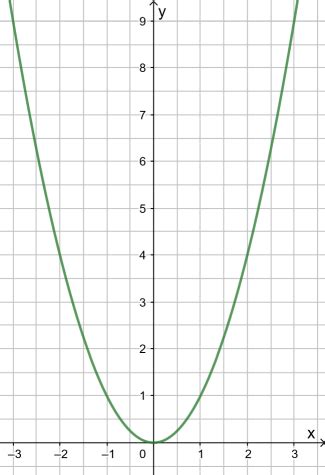
The graph of the equation x² + 1 = x² is a parabola that opens upward. The vertex of the parabola is at the point (0, 1). The parabola intersects the x-axis at the points (-1, 0) and (1, 0).
Equation of the Parabola
The equation of a parabola that opens upward is:
y = ax² + bx + c
where a, b, and c are constants. For the parabola that is the graph of the equation x² + 1 = x², the values of a, b, and c are:
- a = 1
- b = 0
- c = 1
Vertex of the Parabola
The vertex of a parabola is the point where the parabola changes direction. For a parabola that opens upward, the vertex is the lowest point on the parabola. The vertex of the parabola that is the graph of the equation x² + 1 = x² is at the point (0, 1).
Intercepts of the Parabola
The intercepts of a parabola are the points where the parabola intersects the x-axis and the y-axis. The parabola that is the graph of the equation x² + 1 = x² intersects the x-axis at the points (-1, 0) and (1, 0). The parabola does not intersect the y-axis.
Applications
The graph of the equation x² + 1 = x² has many applications in science, engineering, and mathematics. Some of the most common applications include:
- Projectile motion: The graph of the equation x² + 1 = x² can be used to model the trajectory of a projectile. The x-axis represents the horizontal distance traveled by the projectile, and the y-axis represents the vertical height of the projectile. The graph can be used to determine the maximum height reached by the projectile, the distance traveled by the projectile, and the time of flight of the projectile.
- Electrical circuits: The graph of the equation x² + 1 = x² can be used to model the voltage-current relationship in an electrical circuit. The x-axis represents the current flowing through the circuit, and the y-axis represents the voltage drop across the circuit. The graph can be used to determine the resistance of the circuit, the power dissipated by the circuit, and the efficiency of the circuit.
- Mechanical vibrations: The graph of the equation x² + 1 = x² can be used to model the vibrations of a mechanical system. The x-axis represents the displacement of the system from its equilibrium position, and the y-axis represents the velocity of the system. The graph can be used to determine the frequency of the vibrations, the amplitude of the vibrations, and the damping ratio of the system.
Conclusion
The graph of the equation x² + 1 = x² is a parabola that opens upward. The vertex of the parabola is at the point (0, 1). The parabola intersects the x-axis at the points (-1, 0) and (1, 0). The graph of the equation x² + 1 = x² has many applications in science, engineering, and mathematics.