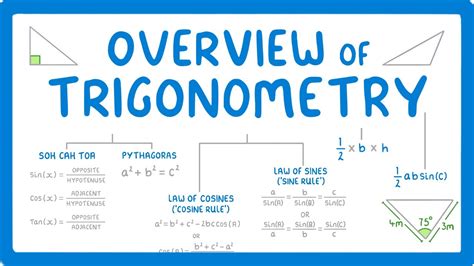
Trigonometry, the enchanting realm of triangles, angles, and trigonometric functions, has captivated the minds of mathematicians and scientists for centuries. Its applications span across a vast array of fields, from engineering and physics to astronomy and navigation. To navigate this intriguing subject with confidence, make sure you master these essential concepts.

1. The Fundamental Concepts of Trigonometry
Angles and Units:
– Angles are measured in degrees (°), radians (rad), or gradians (grads).
– 1° = (π/180) rad ≈ 0.01745 rad
– 1 rad = 180°/π ≈ 57.296°
– 1 grad = (π/200) rad ≈ 9/10°
Trigonometric Functions:
– Sine (sin), Cosine (cos), and Tangent (tan) are the primary trigonometric functions.
– They relate the lengths of sides and angles in right triangles:
– sin(θ) = opposite/hypotenuse
– cos(θ) = adjacent/hypotenuse
– tan(θ) = opposite/adjacent
2. The Unit Circle and Special Angles
The unit circle, with radius 1 centered at the origin, plays a crucial role in trigonometry. Special angles, such as 30°, 45°, and 60°, have well-defined trigonometric values:
| Angle | sin | cos | tan |
|---|---|---|---|
| 0° | 0 | 1 | 0 |
| 30° | 1/2 | √3/2 | √3/3 |
| 45° | √2/2 | √2/2 | 1 |
| 60° | √3/2 | 1/2 | √3 |
| 90° | 1 | 0 | undefined |
3. Solving Triangles
Law of Sines:
– Used to solve triangles when we know two sides and an angle that is not included between them.
– (a/sin A) = (b/sin B) = (c/sin C)
Law of Cosines:
– Used to solve triangles when we know two sides and the angle between them.
– a² = b² + c² – 2bc cos A
4. Applications of Trigonometry
Engineering:
– Designing bridges, buildings, and machines
– Analyzing forces and moments
Physics:
– Calculating projectile motion, oscillations, and wave properties
– Describing the behavior of light and sound
Astronomy:
– Measuring the distances to stars and planets
– Calculating the orbits of celestial bodies
Navigation:
– Determining the position of ships and planes
– Calculating the shortest route between two points
5. Advanced Topics in Trigonometry
Hyperbolic Functions:
– Analogous to trigonometric functions but used in hyperbolic geometry.
Inverse Trigonometric Functions:
– Functions that undo the trigonometric functions.
– arcsin(x), arccos(x), arctan(x)
Complex Numbers in Trigonometry:
– Trigonometric functions can be extended to complex numbers.
6. Common Trigonometric Identities
- Pythagorean Identity: sin²θ + cos²θ = 1
-
Double-Angle Identities:
- sin(2θ) = 2 sin θ cos θ
- cos(2θ) = cos² θ – sin² θ
-
Half-Angle Identities:
- sin(θ/2) = ±√((1 – cos θ)/2)
- cos(θ/2) = ±√((1 + cos θ)/2)
-
Sum and Difference Identities:
- sin(α ± β) = sin α cos β ± cos α sin β
- cos(α ± β) = cos α cos β ∓ sin α sin β
7. Frequently Asked Questions
Question: What are the most important formulas to remember in trigonometry?
Answer: Pythagorean Identity, Double-Angle Identities, Half-Angle Identities, Sum and Difference Identities
Question: How do you solve a right triangle?
Answer: Use the trigonometric functions or the Pythagorean Theorem.
Question: What is the inverse of the sine function?
Answer: The arcsine function (arcsin)
Question: What are the applications of trigonometry in engineering?
Answer: Designing bridges, buildings, and analyzing forces and moments
Question: How is trigonometry used in physics?
Answer: Calculating projectile motion, oscillations, wave properties, and the behavior of light and sound
8. Conclusion
Trigonometry is a captivating subject that unravels the secrets of triangles. By understanding its fundamental concepts, solving triangles, and exploring its applications, you will unlock a powerful tool for solving problems in a multitude of fields. Embrace the beauty and versatility of trigonometry, and conquer the world of triangles with confidence and mastery.