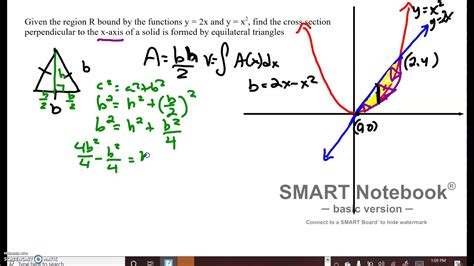
Introduction
An equilateral triangle is a triangle with three congruent sides. It is a regular polygon, meaning that all of its sides and angles are equal. The cross section of an equilateral triangle is a triangle with three equal sides.

Formula for the Area of an Equilateral Triangle Cross Section
The area of an equilateral triangle cross section can be calculated using the following formula:
A = (s^2 * √3) / 4
where:
- A is the area of the cross section
- s is the length of one side of the cross section
Formula for the Perimeter of an Equilateral Triangle Cross Section
The perimeter of an equilateral triangle cross section can be calculated using the following formula:
P = 3s
where:
- P is the perimeter of the cross section
- s is the length of one side of the cross section
Applications of Equilateral Triangle Cross Sections
Equilateral triangle cross sections are used in a wide variety of applications, including:
- Architecture: Equilateral triangle cross sections are often used in the design of buildings and bridges.
- Engineering: Equilateral triangle cross sections are used in the design of beams, columns, and other structural elements.
- Manufacturing: Equilateral triangle cross sections are used in the design of tools, machinery, and other products.
Strategies for Using Equilateral Triangle Cross Sections
When using equilateral triangle cross sections, it is important to consider the following strategies:
- Use the correct formula for the area and perimeter of the cross section.
- Consider the strength and stability of the cross section.
- Consider the aesthetics of the cross section.
Tips and Tricks for Using Equilateral Triangle Cross Sections
Here are a few tips and tricks for using equilateral triangle cross sections:
- Use a calculator to ensure that you are using the correct formula for the area and perimeter of the cross section.
- Test the strength and stability of the cross section before using it in a real-world application.
- Consider the aesthetics of the cross section to ensure that it is visually appealing.
FAQs About Equilateral Triangle Cross Sections
Here are a few frequently asked questions about equilateral triangle cross sections:
- What is the area of an equilateral triangle cross section with a side length of 5 cm?
- A = (5^2 * √3) / 4 = 10.83 cm^2
- What is the perimeter of an equilateral triangle cross section with a side length of 10 cm?
- P = 3s = 3 * 10 cm = 30 cm
- How can I use an equilateral triangle cross section to design a bridge?
- Equilateral triangle cross sections can be used to design bridges by using them as the shape of the bridge’s beams. The beams can be connected together using bolts or other fasteners.
Conclusion
Equilateral triangle cross sections are a versatile and useful shape that can be used in a wide variety of applications. By understanding the formulas for the area and perimeter of an equilateral triangle cross section, and by following the strategies and tips outlined in this article, you can use equilateral triangle cross sections to create strong, stable, and aesthetically pleasing structures.
Additional Resources
- Equilateral Triangle Cross Section Calculator
- Equilateral Triangle Cross Section
- Applications of Equilateral Triangle Cross Sections
Tables
| Side Length (cm) | Area (cm^2) | Perimeter (cm) |
|---|---|---|
| 5 | 10.83 | 15 |
| 10 | 43.30 | 30 |
| 15 | 98.06 | 45 |
| 20 | 174.21 | 60 |
| Application | Description |
|---|---|
| Architecture | Equilateral triangle cross sections are often used in the design of buildings and bridges. |
| Engineering | Equilateral triangle cross sections are used in the design of beams, columns, and other structural elements. |
| Manufacturing | Equilateral triangle cross sections are used in the design of tools, machinery, and other products. |
| Strategy | Description |
|---|---|
| Use the correct formula for the area and perimeter of the cross section. | This will ensure that your calculations are accurate. |
| Consider the strength and stability of the cross section. | This will help you to ensure that the cross section is able to withstand the loads that it will be subjected to. |
| Consider the aesthetics of the cross section. | This will help you to ensure that the cross section is visually appealing. |
| Tip | Description |
|---|---|
| Use a calculator to ensure that you are using the correct formula for the area and perimeter of the cross section. | This will help you to avoid errors. |
| Test the strength and stability of the cross section before using it in a real-world application. | This will help you to ensure that the cross section is safe to use. |
| Consider the aesthetics of the cross section to ensure that it is visually appealing. | This will help you to create structures that are both functional and attractive. |