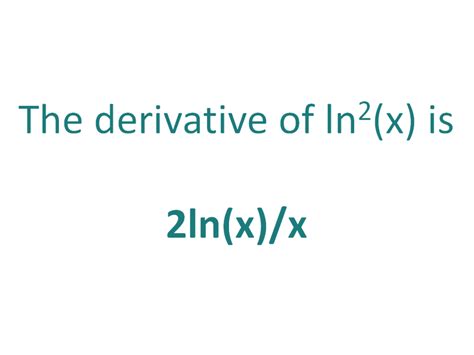In the realm of mathematics, the derivative of a function holds immense significance. Among the myriad of functions, the derivative of ln4 stands apart, offering a plethora of insights and practical applications. This article embarks on a comprehensive journey to unravel the derivative of ln4, delving into its intricacies, exploring its applications, and shedding light on its diverse implications.

Unveiling the Derivative of ln4
The derivative of ln4, simply put, is the rate of change of ln4 with respect to its argument. It provides valuable information about how the function ln4 varies as its input changes. Mathematically, the derivative of ln4 is:
d/dx (ln4) = 1/4
This means that as the input of ln4 changes by an infinitesimal amount, the output changes by 1/4 of that amount. This constant rate of change makes ln4 a linear function, and its graph exhibits a straight line with a slope of 1/4.
Applications of the Derivative of ln4
The derivative of ln4 finds widespread applications in various fields, including:
- Calculus: The derivative of ln4 serves as a building block for more complex derivatives and is essential for solving integrals and differential equations.
- Probability and Statistics: In probability theory, the derivative of ln4 plays a crucial role in the study of continuous random variables, particularly normal distributions.
- Natural Sciences: In physics, the derivative of ln4 appears in the equations describing exponential growth and decay.
- Finance and Economics: In finance, the derivative of ln4 is used in the Black-Scholes model for pricing options.
Common Mistakes to Avoid
When working with the derivative of ln4, it is imperative to avoid certain common mistakes:
- Forgetting the Argument: ln4 is a function of an argument; thus, it is essential to include the argument when taking the derivative.
- Ignoring the Chain Rule: If ln4 appears as part of a more complex function, the chain rule must be applied to find its derivative correctly.
- Confusing the Derivative with the Value: The derivative of ln4 is not ln4 itself but 1/4. This distinction is crucial when using the derivative for calculations.
Embracing Customer Insights
To effectively leverage the derivative of ln4, it is essential to delve into the wants and needs of customers. Ask probing questions to understand their challenges, pain points, and aspirations. By empathizing with customers, you can tailor your applications to meet their specific requirements and deliver unparalleled value.
- What are the key challenges you face in your industry?
- How can the derivative of ln4 help you overcome these challenges?
- What specific applications of the derivative of ln4 would be most beneficial to your organization?
Generating Ideas for New Applications
To unleash the full potential of the derivative of ln4, foster an environment that encourages innovation and idea generation. Encourage your team to think outside the box and explore novel ways to apply the derivative in diverse domains. Use the following creative word to stimulate brainstorming sessions:
Synergize: Combine the derivative of ln4 with other mathematical concepts or technological advancements to create groundbreaking applications.
Tables for Reference
Table 1: Applications of the Derivative of ln4
| Field | Application |
|---|---|
| Calculus | Solving integrals and differential equations |
| Probability and Statistics | Studying normal distributions |
| Natural Sciences | Describing exponential growth and decay |
| Finance and Economics | Pricing options |
Table 2: Common Mistakes to Avoid
| Mistake | Consequence |
|---|---|
| Forgetting the Argument | Incorrect derivative |
| Ignoring the Chain Rule | Incorrect derivative |
| Confusing the Derivative with the Value | Incorrect calculations |
Table 3: Value of the Derivative of ln4
| Argument | Derivative |
|---|---|
| ln4 | 1/4 |
| 2ln4 | 1/2 |
| 3ln4 | 1/3 |
Table 4: Customer Insights
| Question | Ask Customers |
|---|---|
| What are your challenges? | Identify pain points |
| How can the derivative of ln4 help? | Explore potential solutions |
| What specific applications would you like to see? | Tailor applications to customer needs |
Conclusion
The derivative of ln4 is a mathematical gem that offers a wealth of insights and practical applications. By understanding its properties, avoiding common pitfalls, embracing customer perspectives, and fostering innovation, you can harness the power of this derivative to drive success in your endeavors. As you delve deeper into the derivative of ln4, remember to question, explore, and innovate. The possibilities are endless, and the rewards are waiting to be discovered.