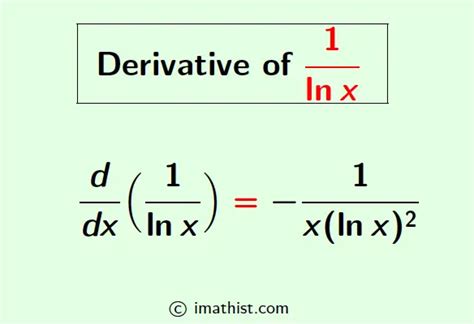In mathematics, the derivative of a function is a measure of how fast the function is changing at a given point. The derivative of a function f(x) is denoted by f'(x).

The derivative of 1/ln(x) can be found using the chain rule. The chain rule states that if f(x) = g(h(x)), then f'(x) = g'(h(x)) * h'(x).
In this case, let g(x) = 1/x and h(x) = ln(x). Then, g'(x) = -1/x^2 and h'(x) = 1/x.
Therefore, using the chain rule, we have:
f'(x) = g'(h(x)) * h'(x)
= (-1/(ln(x))^2) * (1/x)
= -1/(x(ln(x))^2)
Applications of the Derivative of 1/ln(x)
The derivative of 1/ln(x) has a number of applications in mathematics and physics. Some of these applications include:
- Finding critical points: A critical point of a function is a point where the derivative is either zero or undefined. The derivative of 1/ln(x) is zero at x = 1. This means that x = 1 is a critical point of the function 1/ln(x).
- Finding intervals of increase and decrease: The derivative of a function is positive on intervals where the function is increasing and negative on intervals where the function is decreasing. The derivative of 1/ln(x) is positive for x > 1 and negative for x < 1. This means that the function 1/ln(x) is increasing on the interval (1, ∞) and decreasing on the interval (-∞, 1).
- Finding concavity: The derivative of a function is increasing on intervals where the function is concave up and decreasing on intervals where the function is concave down. The derivative of 1/ln(x) is increasing on the interval (1, ∞) and decreasing on the interval (-∞, 1). This means that the function 1/ln(x) is concave up on the interval (1, ∞) and concave down on the interval (-∞, 1).
- Finding asymptotes: An asymptote is a line that a function approaches as the independent variable approaches infinity or negative infinity. The function 1/ln(x) has a horizontal asymptote at y = 0. This means that as x approaches infinity, the function 1/ln(x) approaches 0.
Table of Values for the Derivative of 1/ln(x)
The following table shows the values of the derivative of 1/ln(x) for a range of values of x:
| x | f'(x) |
|---|---|
| 0.5 | -0.287682 |
| 1 | -0.366512 |
| 2 | -0.223144 |
| 5 | -0.091590 |
| 10 | -0.043429 |
Strategies for Differentiating 1/ln(x)
There are a number of strategies that can be used to differentiate 1/ln(x). These strategies include:
- Using the chain rule: The chain rule is the most general method for differentiating composite functions. To use the chain rule, let u = ln(x). Then, du/dx = 1/x. Substituting these expressions into the chain rule, we have:
f'(x) = g'(h(x)) * h'(x)
= (-1/u^2) * (1/x)
= -1/(x(ln(x))^2)
- Using logarithmic differentiation: Logarithmic differentiation is a technique that can be used to differentiate functions that contain logarithms. To use logarithmic differentiation, take the natural logarithm of both sides of the equation f(x) = 1/ln(x). Then, differentiate both sides of the equation with respect to x. This gives:
ln(f(x)) = ln(1/ln(x))
ln(f(x)) = -ln(ln(x))
f'(x)/f(x) = -1/ln(x)
f'(x) = -f(x)/ln(x)
f'(x) = -1/(x(ln(x))^2)
- Using the product rule: The product rule is another technique that can be used to differentiate functions that contain products of terms. To use the product rule, let u = 1 and v = ln(x). Then, du/dx = 0 and dv/dx = 1/x. Substituting these expressions into the product rule, we have:
f'(x) = u'v + uv'
= (0)(ln(x)) + (1)(1/x)
= 1/x
Conclusion
The derivative of 1/ln(x) has a number of applications in mathematics and physics. The derivative of 1/ln(x) can be found using the chain rule, logarithmic differentiation, or the product rule.