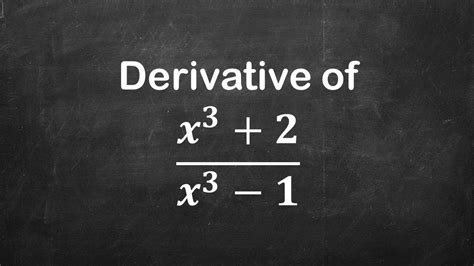Introduction
The derivative of x³ plays a crucial role in various mathematical and scientific applications. This article provides a comprehensive guide to understanding the derivative of x³, its properties, applications, and common mistakes to avoid.

Definition of the Derivative of x³
The derivative of x³ is the function that represents the instantaneous rate of change of y=x³ with respect to x. It is defined as:
dy/dx = d(x³)/dx = 3x²
This means that the slope of the tangent line to the curve y=x³ at any point (x, x³) is 3x².
Properties of the Derivative of x³
The derivative of x³ exhibits the following properties:
- Power rule: The derivative of x³ is equal to 3x², according to the power rule for derivatives.
- Monotonicity: The derivative of x³ is always positive for x ≠ 0. This indicates that the function y=x³ is an increasing function.
- Maximum value: The derivative of x³ reaches a maximum value of 3 at x=1.
Applications of the Derivative of x³
The derivative of x³ finds numerous applications in various fields:
- Optimization: The derivative of x³ is used to find critical points and determine the maximum or minimum values of functions.
- Physics: The derivative of x³ is used to calculate the acceleration of an object moving in a parabolic trajectory.
- Fluid mechanics: The derivative of x³ is used to model the velocity profile of fluid flow in a pipe.
Table 1: Applications of the Derivative of x³
| Field | Application |
|---|---|
| Optimization | Finding critical points and extrema |
| Physics | Calculating acceleration |
| Fluid mechanics | Modeling velocity profile |
Common Mistakes to Avoid
When working with the derivative of x³, it is important to avoid the following common mistakes:
- Sign error: Incorrectly taking the derivative of x³, resulting in -3x² instead of 3x².
- Power rule error: Applying the power rule incorrectly, resulting in 3x instead of 3x².
- Neglecting the constant: Forgetting the multiplicative constant 3 when taking the derivative of x³.
Table 2: Common Mistakes and Corrections
| Mistake | Correction |
|---|---|
| Sign error | Derivative is 3x², not -3x² |
| Power rule error | Derivative is 3x², not 3x |
| Neglecting constant | Derivative is 3x², not x² |
Creative Word: “Parabolicons”
To promote innovative applications of the derivative of x³, we propose the concept of “parabolicons.” Parabolicons are geometrical shapes inspired by the parabolic curves defined by y=x³. These shapes possess unique properties that could lead to novel applications in fields such as engineering, architecture, and design.
Conclusion
The derivative of x³ is a fundamental concept with diverse applications. By understanding its properties, avoiding common mistakes, and exploring new ideas, we can harness its power to solve problems and drive innovation across various disciplines.