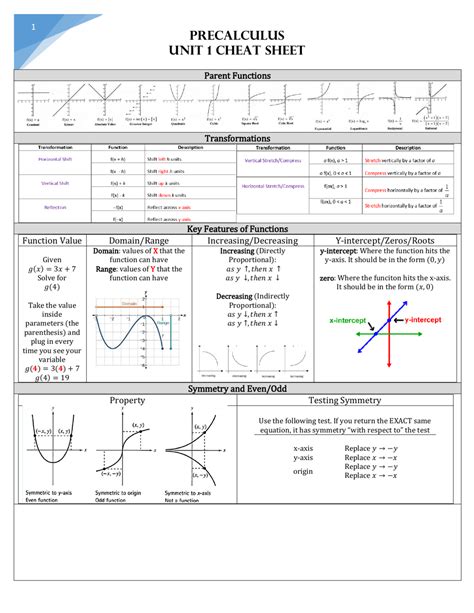
Welcome to the captivating realm of AP Precalculus Unit 1, where you embark on an invigorating journey through the fundamentals of functions, limits, and continuity. Prepare to unravel the intricate tapestry of mathematical concepts that will empower you to tackle complex problems with finesse and precision.

The Enchanting World of Functions: A Framework for Expression
In Unit 1, functions take center stage. Functions provide a powerful language to describe and analyze relationships between variables, opening up a vast array of real-world applications. You will delve into:
-
Function Notation and Terminology: Grasp the essential building blocks of function theory, comprehending concepts such as domain, range, and function evaluation.
-
Graphs of Functions: Visualize the behavior of functions through their graphical representations, discerning patterns and extracting valuable insights.
-
Transformations of Functions: Explore the transformative power of translations, reflections, and dilations, mastering techniques to manipulate graphs effortlessly.
-
Piecewise-Defined Functions: Unravel the complexities of functions that exhibit distinct behaviors over different intervals, honing your ability to analyze and interpret their characteristics.
Limits: Exploring the Boundaries of Infinity and Beyond
Limits, the gatekeepers of calculus, unveil the behavior of functions as their inputs approach specific values. You will conquer:
-
Limits of Functions: Determine the limiting values of functions as their arguments tend towards infinity or specific finite values, unlocking the mysteries of approaching infinity.
-
One-Sided Limits: Investigate the behavior of functions at the endpoints of intervals, understanding the subtle nuances of left-hand and right-hand limits.
-
Infinite Limits: Encounter functions that soar to infinity or plummet to negative infinity, grasping the implications of unbounded behavior.
-
Limits Involving Infinity: Expand your understanding to cases where either the input or output becomes infinite, unraveling the intricacies of asymptotic behavior.
Continuity: Building a Foundation for Calculus
Continuity ensures that functions flow smoothly without abrupt interruptions. You will establish:
-
Continuity of Functions: Define and identify continuous functions, recognizing their ability to represent smooth and continuous relationships.
-
Intermediate Value Theorem: Discover the remarkable property of continuous functions to assume all values between their maximum and minimum values on an interval.
-
Discontinuities: Analyze the nature and types of discontinuities, understanding their impact on the behavior of functions.
-
Removable Discontinuities: Identify and address removable discontinuities, transforming discontinuous functions into continuous ones.
Embark on Your Mathematical Odyssey: Unveiling the Potential of AP Precalculus Unit 1
The concepts explored in AP Precalculus Unit 1 lay the foundation for advanced topics in calculus and beyond. By mastering these fundamentals, you will:
-
Develop a Solid Understanding of Calculus Concepts: Grasp the core ideas underpinning calculus, preparing you for the challenges of higher-level mathematics.
-
Bolster Your Analytical Thinking Skills: Hone your ability to analyze functions, limits, and continuity, fostering critical thinking and problem-solving prowess.
-
Enhance Your Problem-Solving Arsenal: Acquire a toolkit of techniques to tackle complex mathematical problems with confidence and precision.
-
Unlock a World of Applications: Discover the diverse applications of functions, limits, and continuity in fields such as science, engineering, and economics.
Common Pitfalls to Avoid: Navigating the Perils of Unit 1
To ensure your journey through AP Precalculus Unit 1 is smooth and successful, be mindful of these common pitfalls:
-
Misinterpreting Function Notation: Pay meticulous attention to the placement of variables and parentheses in function notation to avoid errors in evaluation.
-
Ignoring Asymptotic Behavior: When calculating limits, consider the behavior of the function as the input approaches infinity or negative infinity to avoid incorrect conclusions.
-
Overlooking Discontinuities: Carefully examine functions for discontinuities, as they can significantly impact their behavior and applications.
-
Relying Solely on Graphs: While graphs provide valuable insights, they can sometimes be misleading. Always consider algebraic and numerical methods to verify your conclusions.
Uncover the Hidden Potential: Applications Beyond the Classroom
The concepts explored in AP Precalculus Unit 1 extend far beyond the classroom, finding applications in a myriad of fields:
-
Modeling Real-World Phenomena: Functions, limits, and continuity serve as powerful tools for modeling diverse phenomena, from population growth to projectile motion.
-
Optimizing Solutions: Limits and derivatives enable the optimization of solutions in science, engineering, and economics, maximizing efficiency and minimizing costs.
-
Predicting Future Events: By understanding the behavior of functions over time, we can make educated predictions and forecast future trends in areas such as finance and weather forecasting.
Inspiring Innovation: Crafting Your Own Applications
The possibilities for applying the concepts of AP Precalculus Unit 1 are limitless. Let your imagination soar and explore novel applications:
-
Design a Motion Sensor: Utilize functions to describe the motion of an object and incorporate limits to detect sudden changes in motion, paving the way for innovative security systems.
-
Optimize Drug Delivery: Leverage functions and limits to model drug concentrations in the body, optimizing dosage schedules to enhance patient outcomes.
-
Create Personalized Learning Experiences: Employ functions and continuity to adapt learning materials to individual student needs, fostering personalized and effective education.
Conclusion: Empowering Your Mathematical Journey
AP Precalculus Unit 1 marks the gateway to a transformative mathematical journey. By mastering the concepts of functions, limits, and continuity, you will unlock a wealth of applications and embark on a path of mathematical empowerment. As you delve deeper into AP Precalculus and beyond, these foundational principles will serve as your trusty companions, guiding you to new heights of mathematical discovery and innovation.
Appendix: Useful Tables for AP Precalculus Unit 1
| Type of Function | Graph | Domain | Range |
|---|---|---|---|
| Constant Function | Horizontal line | All real numbers | Constant value |
| Linear Function | Slanted line | All real numbers | All real numbers |
| Quadratic Function | Parabola | All real numbers | Minimum or maximum value |
| Cubic Function | Cubic curve | All real numbers | All real numbers |
| Exponential Function | Rapidly increasing or decreasing curve | All real numbers | Positive real numbers |
| Logarithmic Function | Reverse of exponential function | Positive real numbers | All real numbers |
| Type of Discontinuity | Definition | Example |
|---|---|---|
| Removable Discontinuity | A discontinuity that can be eliminated by redefining the function at a single point | f(x) = (x – 1)/(x – 2) |
| Jump Discontinuity | A discontinuity where the function has different limits from the left and right | f(x) = |
| Infinite Discontinuity | A discontinuity where the function has an infinite limit | f(x) = 1/x |
| Limit Law | Definition | Example |
|---|---|---|
| Sum Law | lim (a(x) + b(x)) = lim (a(x)) + lim (b(x)) | lim (x^2 + 3x – 2) = lim (x^2) + lim (3x) – lim (2) = ∞ + ∞ – 0 = ∞ |
| Product Law | lim (a(x) * b(x)) = lim (a(x)) * lim (b(x)) | lim (x^2 * sin(x)) = lim (x^2) * lim (sin(x)) = ∞ * 0 = 0 |
| Quotient Law | lim (a(x) / b(x)) = lim (a(x)) / lim (b(x)) | lim (x^2 – 1) / (x – 1) = lim (x^2 – 1) / lim (x – 1) = ∞ / ∞ = 1 |
| Power Law | lim (a(x)^n) = lim (a(x))^n | lim (x^3 – 2x + 1) = lim (x^3 – 2x + 1)^1 = ∞^1 = ∞ |