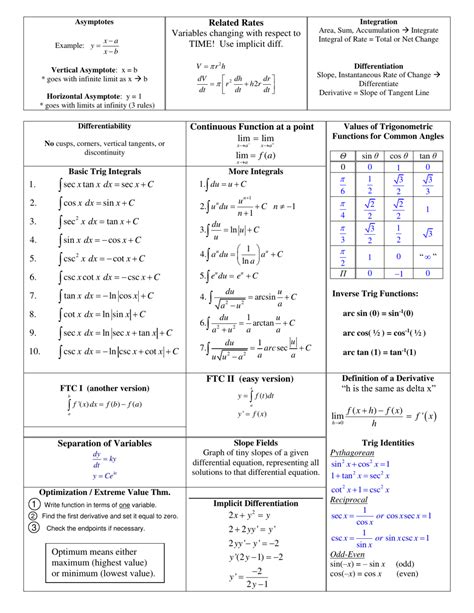
Introduction

Calculus AB is a foundational course in mathematics that introduces students to the concepts of limits, derivatives, and integrals. Mastering these concepts is essential for success in higher-level math and science courses, as well as in many real-world applications. This comprehensive cheat sheet provides a concise and accessible overview of the key formulas, theorems, and techniques from Calculus AB, empowering you to conquer the challenges of this crucial subject.
Limits
- Definition: The limit of a function f(x) as x approaches a is the value L such that for any ε > 0, there exists a δ > 0 such that |f(x) – L| < ε whenever |x - a| < δ.
-
Limit Laws:
- Sum Rule: lim (f(x) + g(x)) = lim f(x) + lim g(x)
- Difference Rule: lim (f(x) – g(x)) = lim f(x) – lim g(x)
- Product Rule: lim (f(x)g(x)) = lim f(x) lim g(x)
- Quotient Rule: lim (f(x)/g(x)) = lim f(x)/lim g(x), provided lim g(x) ≠ 0
-
Indeterminate Forms:
- 0/0: Use L’Hôpital’s Rule or factor out common factors
- ∞/∞: Use L’Hôpital’s Rule or divide by the highest power of x
- 0^0: Rewrite as e^(ln 0^0) or use the Squeeze Theorem
- 1^∞: Rewrite as e^(ln 1^∞) or use the Squeeze Theorem
Derivatives
- Definition: The derivative of a function f(x) is the function f'(x) such that f'(x) = lim (Δf)/(Δx) = lim (f(x + h) – f(x))/(h) as h → 0.
- Power Rule: f(x) = x^n, f'(x) = nx^(n-1)
- Sum Rule: (f + g)'(x) = f'(x) + g'(x)
- Difference Rule: (f – g)'(x) = f'(x) – g'(x)
- Product Rule: (fg)'(x) = f(x)g'(x) + f'(x)g(x)
- Quotient Rule: (f/g)'(x) = (g(x)f'(x) – f(x)g'(x))/(g(x))^2, provided g(x) ≠ 0
- Chain Rule: f(g(x))’, f(g(x))g'(x)
Integrals
- Definition: The indefinite integral of a function f(x) is the function F(x) such that F'(x) = f(x).
- Fundamental Theorem of Calculus (Part 1): If f(x) is continuous on [a, b], then the definite integral of f(x) from a to b is equal to the net area under the curve of f(x) on that interval.
-
Indefinite Integral Rules:
- Power Rule: ∫x^n dx = (x^(n+1))/(n+1) + C, n ≠ -1
- Sum Rule: ∫(f(x) + g(x)) dx = ∫f(x) dx + ∫g(x) dx
- Difference Rule: ∫(f(x) – g(x)) dx = ∫f(x) dx – ∫g(x) dx
- Substitution Rule: ∫f(g(x))g'(x) dx = ∫f(u) du, u = g(x)
- Integration by Parts: ∫uv dx = uv – ∫v du
Applications of Calculus
Calculus has countless applications in various fields, including:
- Physics: Calculating acceleration, velocity, and distance
- Engineering: Designing bridges, buildings, and machines
- Economics: Analyzing market demand and consumer behavior
- Biology: Modeling population growth and epidemic spread
- Medicine: Optimizing drug dosage and treatment plans
Useful Tables
Table 1: Derivative Formulas
| Function | Derivative |
|---|---|
| x^n | nx^(n-1) |
| sin(x) | cos(x) |
| cos(x) | -sin(x) |
| tan(x) | sec^2(x) |
| e^x | e^x |
| ln(x) | 1/x |
Table 2: Integral Formulas
| Function | Indefinite Integral |
|---|---|
| x^n | (x^(n+1))/(n+1) |
| sin(x) | -cos(x) |
| cos(x) | sin(x) |
| tan(x) | ln |
| e^x | e^x |
| ln(x) | x ln(x) – x |
Table 3: Limits of Indeterminate Forms
| Indeterminate Form | Limit |
|---|---|
| 0/0 | lim (f(x)/g(x)) |
| ∞/∞ | lim (f(x)/g(x)) |
| 0^0 | lim (f(x))^g(x) |
| 1^∞ | lim (f(x))^g(x) |
Table 4: Integration Techniques
| Integration Technique | Formula |
|---|---|
| U-Substitution | ∫f(g(x))g'(x) dx = ∫f(u) du |
| Integration by Parts | ∫uv dx = uv – ∫v du |
| Partial Fractions | ∫(ax+b)/(cx^2+dx+e) dx = ∫(A/x+B/(cx+d)+C/(cx^2+dx+e)) dx |
| Trigonometric Identities | sin^2(x) + cos^2(x) = 1, tan^2(x) + 1 = sec^2(x) |
Tips and Tricks
- Understand the concepts: Don’t just memorize formulas; grasp the underlying principles to apply them effectively.
- Practice regularly: Solve numerous problems to enhance your problem-solving skills.
- Seek help when needed: Don’t hesitate to ask for assistance from teachers, tutors, or classmates.
- Use technology wisely: Graphing calculators and computer software can aid in visualizing and solving problems.
- Review previous material: Refresh your knowledge of algebra, trigonometry, and pre-calculus to strengthen your foundation.
Common Mistakes to Avoid
- Forgetting units: Always include appropriate units when solving problems involving rates and measurements.
- Using the wrong formulas: Be careful to select the appropriate formula for each situation.
- Making algebraic errors: Check your calculations thoroughly to avoid mistakes.
- Ignoring limits: Remember to consider the limits of integration when solving integrals.
- Not understanding the problem: Read the problem carefully and identify the key information before attempting to solve it.
FAQs
-
What is the difference between a limit and a derivative?
A limit describes the behavior of a function as the input approaches a certain value, while a derivative measures the instantaneous rate of change of a function. -
How do I know which integration technique to use?
The choice of integration technique depends on the form of the integrand. Common techniques include U-substitution, integration by parts, and partial fractions. -
What are the applications of calculus in real life?
Calculus is used in countless applications, such as calculating rocket trajectories, predicting weather patterns, and optimizing financial portfolios. -
How can I improve my calculus skills?
Practice solving problems regularly, seek help when needed, and review your notes and textbooks thoroughly. -
What are some common mistakes students make in Calculus AB?
Common mistakes include forgetting units, using the wrong formulas, making algebraic errors, ignoring limits, and not understanding the problem statement. -
What are the most important concepts to master in Calculus AB?
Key concepts include limits, derivatives, integrals, the Fundamental Theorem of Calculus, and their applications in various fields. -
How can I prepare for the Calculus AB exam?
Thoroughly review the course material, practice solving problems from previous exams, and seek feedback on your performance from teachers or tutors. -
What is the best way to study for Calculus AB?
A structured study plan, regular problem-solving practice, and active engagement with the material are essential for success in Calculus AB.