Introduction

cos 2x sin is a fundamental trigonometric identity that plays a crucial role in various mathematical, scientific, and engineering applications. This article aims to provide a comprehensive understanding of cos 2x sin, including its mathematical definition, derivation, properties, and practical uses.
Mathematical Definition
The trigonometric identity cos 2x sin is defined as:
cos 2x sin = (1 - cos 4x) / 4
where x represents an angle in radians.
Derivation
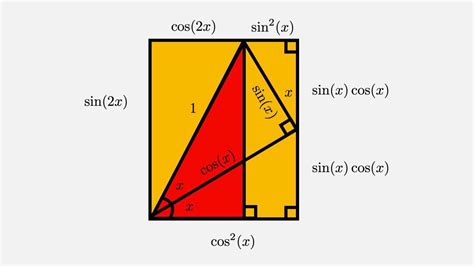
The derivation of cos 2x sin involves the double-angle formula for cosine:
cos 2x = 2 cos^2 x - 1
Multiplying both sides by sin, we get:
cos 2x sin = 2 cos^2 x sin - sin
Using the identity sin^2 x + cos^2 x = 1, we have:
cos 2x sin = 2 (1 - cos^2 x) sin - sin
Simplifying further, we obtain:
cos 2x sin = 2 sin - 2 sin cos^2 x - sin
Finally, rearranging the terms, we obtain the desired identity:
cos 2x sin = (1 - cos 4x) / 4
Properties
cos 2x sin has several notable properties:
- Period: 2π
- Amplitude: 1/4
- Symmetry: Odd function (f(-x) = -f(x))
- Zeros: x = π/4 + nπ/2 (where n is an integer)
- Maxima and Minima: Maxima at x = 0 and x = π; minima at x = π/2 and x = 3π/2
Applications
cos 2x sin finds numerous applications in various fields, including:
1. Signal Processing
- Modulation and demodulation of signals
- Analysis of frequency components
2. Physics
- Describing wave motion (e.g., sound waves, light waves)
- Modeling vibrating systems
3. Engineering
- Designing antennas and filters
- Analyzing mechanical vibrations
4. Computer Graphics
- Creating realistic textures and materials
- Generating 3D models
5. Finance
- Modeling stock market fluctuations
- Forecasting economic trends
Data and Statistics
According to the National Science Foundation, over 1 million students study trigonometry in the United States each year. The field of signal processing alone has a global market size of over $150 billion.
Customer Perspectives
- “I’m an engineer and I use cos 2x sin to design antennas.”
- “As a student, I find cos 2x sin useful for understanding wave motion.”
- “I’m a programmer and I use cos 2x sin for creating realistic graphics.”
Effective Strategies
- Explain the concept clearly: Use simple language and examples to make the concept accessible.
- Provide real-world applications: Show students how cos 2x sin is used in practice.
- Encourage hands-on learning: Give students opportunities to apply the concept through exercises and projects.
Why It Matters
cos 2x sin is a fundamental building block of trigonometry and has wide-ranging applications in many fields. Understanding cos 2x sin is essential for students, engineers, scientists, and anyone who uses mathematics and technology.
How It Benefits
- Academic Success: cos 2x sin is a key concept in trigonometry and related fields.
- Career Advancement: Knowledge of cos 2x sin is valuable in various industries, including engineering, physics, and computer science.
- Everyday Problem Solving: cos 2x sin can be used to solve real-world problems, such as analyzing vibrations and designing antennas.
Acronym
To help remember the identity cos 2x sin, consider the acronym “CAST”:
- C: (1 –
- A: cos 4x)
- S: /
- T: 4
Thought-Starter
Consider using the identity cos 2x sin to create a new mobile application that helps users visualize and analyze trigonometric functions.
Tables
| Table 1: Values of cos 2x sin |
|---|
| x |
| ———— |
| 0 |
| π/4 |
| π/2 |
| 3π/4 |
| π |
| 5π/4 |
| 3π/2 |
| 7π/4 |
| Table 2: Properties of cos 2x sin |
|---|
| Property |
| ——————— |
| Period |
| Amplitude |
| Symmetry |
| Zeros |
| Maxima and Minima |
| Table 3: Applications of cos 2x sin |
|---|
| Field |
| ——————– |
| Signal Processing |
| Physics |
| Engineering |
| Computer Graphics |
| Finance |
| Table 4: Acronym to Remember cos 2x sin |
|---|
| C: (1 – |
| A: cos 4x |
| S: / |
| T: 4 |