The SAT, a standardized test widely used for college admissions, often includes questions involving slant height, a crucial concept in geometry. Understanding slant height and its applications is essential for maximizing your score on the SAT. This comprehensive guide will provide you with a thorough understanding of slant height, including its definition, formulas, and strategies for solving SAT questions related to it.

What is Slant Height?
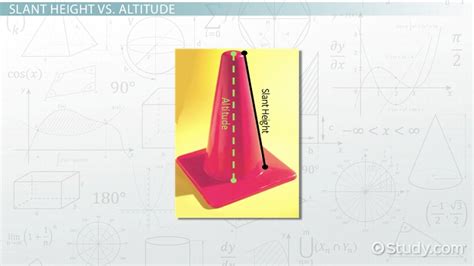
Slant height refers to the length of the segment connecting the apex of a cone or pyramid to the base’s circumference. It represents the shortest distance from the apex to any point on the base. In the case of a right cone, the slant height forms a right triangle with the radius of the base and the height of the cone.
Formulas for Slant Height
- **Cone:** Slant height = √(Height² + Radius²)
- **Pyramid:** Slant height = √(Height² + (1/2 * Base Side)²) for a square or rectangular base
Effective Strategies for SAT Questions
- Identify the type of shape: Determine whether the question pertains to a cone or a pyramid.
- Locate the given measurements: Identify the provided values for height and radius (cone) or height and base side (pyramid).
- Apply the appropriate formula: Substitute the given values into the correct formula for slant height.
- Simplify and calculate: Perform the necessary calculations to obtain the slant height.
- Check your answer: Verify your result by plugging it back into the formula and ensuring that it aligns with the given measurements.
Common Mistakes to Avoid
- Using the wrong formula: Ensure that you use the correct formula for the specific shape involved.
- Misinterpreting the given measurements: Pay attention to the units of measurement and ensure that you interpret them correctly.
- Rounding errors: Avoid rounding intermediate values, as this can affect the accuracy of your final answer.
Pros and Cons of Using Slant Height
Pros:
- Provides a direct measurement of the distance from the apex to the base.
- Simplifies calculations involving three-dimensional shapes.
Cons:
- Can be complex to calculate for irregular bases.
- May not always be the most intuitive measurement to use.
Innovative Applications of Slant Height
Beyond the SAT, slant height finds practical applications in various domains:
- Architecture: Designing roofs, spires, and other structural components with optimal angles and stability.
- Engineering: Calculating the volume and surface area of containers and other objects with conical or pyramidal shapes.
- Physics: Determining the force exerted by a fluid on a submerged object with a conical or pyramidal shape.
Additional Resources
- Khan Academy: Slant Height of a Cone
- Mathway: Slant Height Calculator
- Varsity Tutors: Slant Height on the SAT
Conclusion
Slant height is an indispensable concept in geometry, particularly in relation to cones and pyramids. By understanding its definition, formulas, and effective strategies for SAT questions, students can confidently approach these problems and maximize their scores. Moreover, its applications extend beyond standardized testing, revealing its versatility in diverse fields such as architecture, engineering, and physics.