In the realm of celestial mechanics, Johannes Kepler’s three laws of planetary motion have played a pivotal role in our understanding of the universe. Derived from meticulous observations of the planets, these laws provide a fundamental framework for comprehending the dynamics of celestial bodies. This article presents a collection of simple practice problems that will help you solidify your grasp of Kepler’s laws and apply them to real-world scenarios.

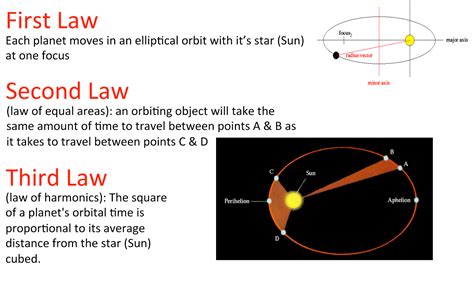
Law 1: The Law of Ellipses
Each planet, including Earth, moves in an elliptical orbit around the Sun, with the Sun located at one of the foci of the ellipse.
Law 2: The Law of Equal Areas
A line connecting a planet to the Sun sweeps out equal areas in equal intervals of time. This implies that a planet moves faster when closer to the Sun, while it slows down when farther away.
Law 3: The Law of Harmonies
The square of a planet’s orbital period is proportional to the cube of its average distance from the Sun. In other words, the farther a planet is from the Sun, the longer it takes to complete one orbit.
Problem 1: Identifying Elliptical Orbits
Question: The eccentricity of an orbit is a measure of its elongation. An eccentricity of 0 represents a circular orbit, while a value closer to 1 indicates a more elongated orbit. If the eccentricity of a planet’s orbit is 0.25, what type of orbit does the planet follow?
Solution: The eccentricity value indicates an elongated orbit. The planet follows an elliptical orbit.
Problem 2: Applying the Law of Equal Areas
Question: A spacecraft is in orbit around Earth. At its closest point to Earth, the spacecraft is 400 km above the planet’s surface. When the spacecraft is at its farthest point from Earth, how far above the surface is it? (Assume a circular orbit with a radius of 6,378 km.)
Solution:
Time to sweep out equal areas: t
Distance traveled in time t at closest point: 2π(400 km)
Distance traveled in time t at farthest point: 2π(x)
By the law of equal areas:
2π(400 km) = 2π(x)
Solving for x:
x = 400 km
The spacecraft is 400 km above the surface at its farthest point.
Problem 3: Using the Law of Harmonies
Question: Jupiter has an orbital period of 11.86 Earth years. How long would it take for a hypothetical planet with an average distance from the Sun of 10 AU to complete one orbit?
Solution:
Jupiter's orbital period (P1) = 11.86 Earth years
Jupiter's average distance from the Sun (r1) = 5.2 AU
Hypothetical planet's average distance from the Sun (r2) = 10 AU
Using the law of harmonies:
(P1²/r1³) = (P2²/r2³)
Solving for P2:
P2 = P1 * (r2³/r1³)
P2 = 11.86 years * (10³/5.2³)
P2 = 29.46 years
The hypothetical planet would take approximately 29.46 years to complete one orbit.
- Misinterpreting the Law of Ellipses: The Sun is not always located at the center of an ellipse. Instead, it is situated at one of the two foci.
- Oversimplifying the Law of Equal Areas: This law applies only to the area swept out by a line connecting the planet to the Sun. It does not mean that the planet moves at a constant speed.
- Applying the Law of Harmonies Incorrectly: This law relates the orbital period to the average distance from the Sun, not the maximum or minimum distance.
The principles underlying Kepler’s laws have far-reaching implications in various fields:
- Space Exploration: Spacecraft are designed to enter orbit around planets and moons using these laws.
- Astrophysics: The properties of exoplanets can be inferred from their observed orbits.
- Engineering: The concept of elliptical paths is used in the design of roller coasters and other amusement park rides.
Kepler’s laws provide a robust framework for understanding planetary motion. By engaging in practice problems, you can deepen your comprehension of these laws and appreciate their practical applications. Whether you aspire to unravel the mysteries of the cosmos or harness their principles for engineering marvels, Kepler’s laws remain an indispensable foundation for your celestial endeavors.
Table 1: Orbital Parameters of Planets in Our Solar System
| Planet | Semi-Major Axis (AU) | Eccentricity | Orbital Period (Earth years) |
|---|---|---|---|
| Mercury | 0.387 | 0.206 | 0.241 |
| Venus | 0.723 | 0.007 | 0.615 |
| Earth | 1.000 | 0.017 | 1.000 |
| Mars | 1.524 | 0.093 | 1.881 |
| Jupiter | 5.203 | 0.048 | 11.86 |
Table 2: Kepler’s Laws and Their Applications
| Kepler’s Law | Application |
|---|---|
| Law of Ellipses | Designing roller coasters |
| Law of Equal Areas | Predicting spacecraft trajectories |
| Law of Harmonies | Estimating the orbital period of exoplanets |
Table 3: Common Mistakes in Applying Kepler’s Laws
| Mistake | Explanation |
|---|---|
| Confusing the center of an ellipse with the Sun | The Sun is located at one of the foci of the ellipse. |
| Assuming a constant speed for a planet | The planet’s speed varies as it moves along its orbit. |
| Applying the Law of Harmonies to the maximum or minimum distance from the Sun | The law applies to the average distance from the Sun. |
Table 4: Kepler’s Laws and Related Engineering Concepts
| Kepler’s Law | Engineering Concept |
|---|---|
| Law of Ellipses | Elliptical gears |
| Law of Equal Areas | Cam and follower mechanisms |
| Law of Harmonies | Harmonic oscillators |