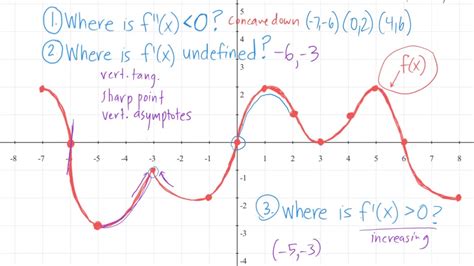
In calculus, finding the graph of a function f(x) given its derivative f'(x) is a fundamental task. The derivative of a function provides valuable information about its rate of change, which can be leveraged to construct the original function’s graph.

Understanding the Relationship Between f(x) and f'(x)
The derivative of a function f(x) with respect to x, denoted as f'(x), measures the instantaneous rate of change of f(x) at any given point x. Geometrically, f'(x) represents the slope of the tangent line to the graph of f(x) at the point (x, f(x)).
Key Relationship:
- If f'(x) > 0, f(x) is increasing.
- If f'(x) < 0, f(x) is decreasing.
- If f'(x) = 0, f(x) has a local maximum or minimum.
Methods to Find f(x) from f'(x)
1. Antidifferentiation
The most direct way to find f(x) from f'(x) is to apply antidifferentiation. Antidifferentiation is the inverse operation of differentiation, and it involves finding a function whose derivative is the given function.
Process:
- Integrate f'(x) with respect to x, which yields F(x) + C, where F(x) is the antiderivative of f'(x) and C is a constant of integration.
- Find the value of C by using an initial condition or a known point on the graph of f(x).
2. Graphical Integration
For functions with relatively simple derivatives, graphical integration can be an intuitive approach.
Process:
- Plot the graph of f'(x).
- Divide the graph into small intervals.
- For each interval, estimate the average value of f'(x).
- Multiply the average value by the length of the interval to obtain the approximate area under the curve of f'(x) within that interval.
- Sum the areas for all intervals to obtain the estimated value of F(x) + C.
- Use an initial condition to find the value of C.
Applications of Finding f(x) from f'(x)
Finding the graph of f(x) from f'(x) has numerous applications in real-world scenarios and scientific research:
- Motion Analysis: Given the velocity function v(t), finding the displacement function s(t) involves antidifferentiating v(t).
- Optimization: Determining the maximum or minimum of a function f(x) involves finding the values of x where f'(x) = 0.
- Fluid Dynamics: Modeling the flow of fluids requires understanding the velocity and acceleration fields, which can be derived from the derivatives of the stream function.
- Circuit Analysis: Finding the charge or current in an electrical circuit involves integrating the voltage or current functions.
Tips and Tricks
- Use Symmetry: If f'(x) is an odd function, f(x) will be an even function, and vice versa.
- Look for Patterns: Examine the behavior of f'(x) to identify patterns that may simplify the antidifferentiation process.
- Change of Variables: Consider using u-substitution or other change of variables techniques to simplify the integration.
- Numerical Methods: If analytical antidifferentiation is not feasible, numerical integration methods such as the trapezoidal rule or Simpson’s rule can be employed.
Conclusion
Finding the graph of f(x) given f'(x) is a crucial skill in calculus. By understanding the relationship between the two functions and employing appropriate techniques, students and researchers can effectively construct the original function’s graph and unlock valuable insights into its behavior.