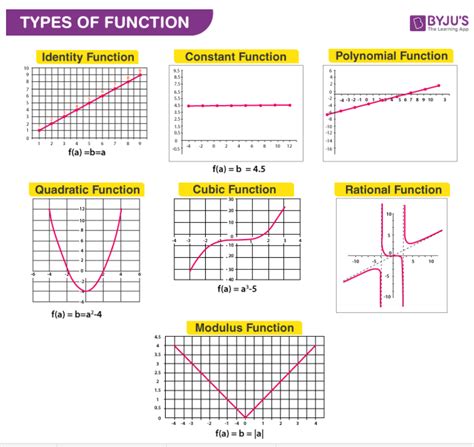
A function is a relation between a set of inputs and a set of outputs, with the property that each input is associated with exactly one output. In other words, a function is a rule that assigns to each element of a set a unique element of another set.

A graph is a visual representation of a relation. It consists of a set of points, each of which represents an input-output pair. The input is typically plotted on the horizontal axis, and the output is plotted on the vertical axis.
A graph is not a function if there is at least one input that is associated with two or more outputs. In other words, if there is at least one point on the graph that has a vertical line passing through it, then the graph is not a function.
Consider the following graph:
[Image of a graph with two vertical lines passing through the point (1, 2)]
The graph is not a function because the input value 1 is associated with two different output values, 2 and 3. This is indicated by the two vertical lines passing through the point (1, 2).
Functions have a number of important properties. These properties include:
- Each input is associated with exactly one output. This is the defining property of a function.
- The graph of a function is a vertical line. This is because each input is associated with exactly one output.
- The inverse of a function is also a function. The inverse of a function is a function that undoes the original function.
Functions have a wide variety of applications in mathematics, science, and engineering. Some of these applications include:
- Modeling physical phenomena. Functions can be used to model a wide variety of physical phenomena, such as the motion of objects, the flow of fluids, and the growth of populations.
- Solving problems. Functions can be used to solve a wide variety of problems, such as finding the area of a region, the volume of a solid, and the roots of an equation.
- Creating computer graphics. Functions can be used to create a wide variety of computer graphics, such as images, animations, and games.
There are a number of common mistakes that people make when working with functions. These mistakes include:
- Mistaking a relation for a function. A relation is a set of input-output pairs, but it is not necessarily a function. A function is a relation that has the property that each input is associated with exactly one output.
- Assuming that the graph of a function is a straight line. The graph of a function is not always a straight line. In fact, the graph of a function can be any shape.
- Using the inverse of a function without checking that the function is invertible. The inverse of a function is only a function if the original function is one-to-one.
Here are some of the most frequently asked questions about functions:
- What is the difference between a function and a relation? A relation is a set of input-output pairs, while a function is a relation that has the property that each input is associated with exactly one output.
- What is the graph of a function? The graph of a function is a visual representation of the function. It consists of a set of points, each of which represents an input-output pair.
-
What are the properties of functions? Functions have a number of important properties, including the following:
- Each input is associated with exactly one output.
- The graph of a function is a vertical line.
- The inverse of a function is also a function.
-
What are some applications of functions? Functions have a wide variety of applications in mathematics, science, and engineering. Some of these applications include:
- Modeling physical phenomena.
- Solving problems.
- Creating computer graphics.
-
What are some common mistakes to avoid when working with functions? There are a number of common mistakes that people make when working with functions. These mistakes include:
- Mistaking a relation for a function.
- Assuming that the graph of a function is a straight line.
- Using the inverse of a function without checking that the function is invertible.