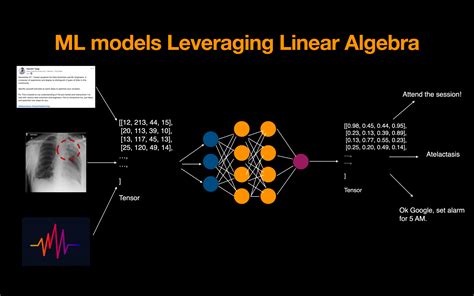
Yes, linear algebra is extensively used in statistics. It provides a mathematical framework for representing, manipulating, and analyzing data in a way that is both efficient and insightful. Linear algebra concepts such as vectors, matrices, and transformations are essential for tasks like:

- Linear regression: Modeling relationships between variables using straight lines or planes.
- Principal component analysis (PCA): Reducing data dimensionality and identifying patterns.
- Discriminant analysis: Classifying data points into distinct groups.
- Analysis of variance (ANOVA): Testing for differences between means of multiple groups.
- Time series analysis: Forecasting future values of a time-dependent variable.
Applications of Linear Algebra in Statistics
Linear algebra finds applications in various statistical fields, including:
- Biostatistics: Modeling clinical trials and genomic data.
- Econometrics: Analyzing economic time series and financial data.
- Machine learning: Developing algorithms for tasks like classification, regression, and clustering.
- Social sciences: Studying social networks and analyzing survey data.
According to a study by the American Statistical Association, over 80% of statisticians use linear algebra in their daily work. This reflects the importance of linear algebra as a fundamental skill for statistical analysis.
Benefits of Using Linear Algebra in Statistics
The use of linear algebra in statistics offers numerous benefits:
- Efficiency: Linear algebra provides efficient algorithms for solving statistical problems.
- Generalizability: Linear algebra concepts can be applied to a wide range of data types and statistical models.
- Interpretability: Results from linear algebra-based analysis can often be easily interpreted in terms of real-world phenomena.
Tables for Reference
Table 1: Linear Algebra Concepts Used in Statistics
| Concept | Description |
|---|---|
| Vector | An ordered collection of numbers |
| Matrix | A rectangular array of numbers |
| Transformation | A mapping that converts one vector or matrix to another |
| Linear combination | A sum of vectors multiplied by scalars |
| Eigenvalue | A scalar that represents the scaling factor of a vector under a transformation |
| Eigenvector | A vector that is scaled by its eigenvalue under a transformation |
Table 2: Statistical Techniques That Use Linear Algebra
| Technique | Purpose | Linear Algebra Concept |
|---|---|---|
| Linear regression | Modeling linear relationships | Linear equations and matrices |
| PCA | Dimensionality reduction | Eigenvalues and eigenvectors |
| Discriminant analysis | Classification | Linear transformations and projection |
| ANOVA | Testing for group differences | Matrices and matrix operations |
| Time series analysis | Forecasting future values | Matrix algebra and transformations |
Table 3: Applications of Linear Algebra in Statistics
| Field | Application |
|---|---|
| Biostatistics | Clinical trial design and analysis |
| Econometrics | Economic modeling and forecasting |
| Machine learning | Classification, regression, and clustering |
| Social sciences | Network analysis and survey data analysis |
Table 4: Benefits of Using Linear Algebra in Statistics
| Benefit | Explanation |
|---|---|
| Efficiency | Solves problems quickly and effectively |
| Generalizability | Applicable to various data types and models |
| Interpretability | Results can be explained in real-world terms |
Conclusion
Linear algebra is an indispensable tool for statisticians, providing a mathematical framework for data representation, analysis, and modeling. Its extensive applications in various statistical fields demonstrate its importance as a fundamental skill for statistical analysis and research.