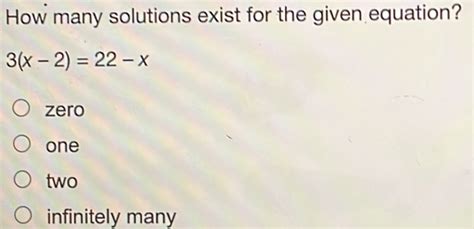In mathematics, an equation is a statement that two expressions are equal. When solving an equation, the goal is to find the values of the variables that make the equation true. The number of solutions to an equation can vary depending on the type of equation.

Linear Equations
Linear equations are equations that can be written in the form Ax + B = C, where A, B, and C are constants. Linear equations have only one solution. This can be seen by solving the equation for x:
Ax + B = C
Ax = C – B
x = (C – B) / A
Therefore, the solution to a linear equation is a single number.
Quadratic Equations
Quadratic equations are equations that can be written in the form Ax^2 + Bx + C = 0, where A, B, and C are constants. Quadratic equations can have two solutions, one solution, or no solutions. The number of solutions can be determined by calculating the discriminant, which is given by the formula B^2 – 4AC.
- If the discriminant is positive, there are two solutions.
- If the discriminant is zero, there is one solution.
- If the discriminant is negative, there are no solutions.
Cubic Equations
Cubic equations are equations that can be written in the form Ax^3 + Bx^2 + Cx + D = 0, where A, B, C, and D are constants. Cubic equations can have three solutions, two solutions, one solution, or no solutions. The number of solutions can be determined by calculating the discriminant, which is given by a complicated formula.
Quartic Equations
Quartic equations are equations that can be written in the form Ax^4 + Bx^3 + Cx^2 + Dx + E = 0, where A, B, C, D, and E are constants. Quartic equations can have four solutions, three solutions, two solutions, one solution, or no solutions. The number of solutions can be determined by calculating the discriminant, which is given by an even more complicated formula.
Common Mistakes to Avoid
When solving equations, it is important to avoid the following common mistakes:
- Forgetting to check for extraneous solutions. Extraneous solutions are solutions that satisfy the equation but do not make sense in the context of the problem. For example, if you are solving the equation x^2 = 4, the solution x = -2 is extraneous because it does not make sense to have a negative square root.
- Dividing by zero. Dividing by zero is undefined, so you should never divide by zero when solving an equation.
- Using the wrong operations. When solving an equation, it is important to use the correct operations. For example, if you are solving the equation x + 5 = 10, you should subtract 5 from both sides of the equation, not divide by 5.
Step-by-Step Approach
To solve an equation, you can follow these steps:
- Simplify the equation by combining like terms and moving all the constants to one side of the equation.
- Solve the equation for the variable.
- Check your solution by plugging it back into the original equation.
FAQs
Here are some frequently asked questions about solving equations:
- How do I know if an equation has a solution? An equation has a solution if the value of the variable makes the equation true.
- How many solutions can an equation have? An equation can have one solution, two solutions, three solutions, or no solutions.
- What is the discriminant? The discriminant is a number that can be used to determine the number of solutions to a quadratic equation.
- How do I check my solution to an equation? You can check your solution by plugging it back into the original equation.
Conclusion
Solving equations is a fundamental skill in mathematics. By understanding the different types of equations and the methods for solving them, you can solve any equation that you encounter.