Introduction
In AP Psychology, understanding the correlation coefficient is fundamental to analyzing and interpreting relationships between variables. This numerical measure determines the extent to which two variables are associated, providing valuable insights into causal relationships and making predictions about future outcomes.

Definition
The correlation coefficient, denoted as ‘r’, measures the linear association between two variables. It ranges from -1 to 1, with:
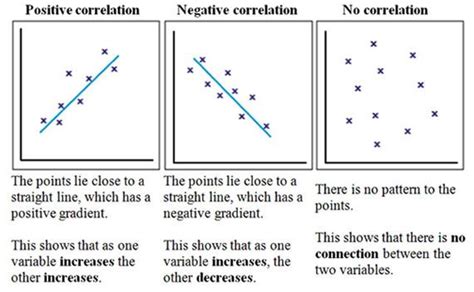
- Negative correlation (r < 0): As one variable increases, the other variable decreases.
- Positive correlation (r > 0): As one variable increases, the other variable also increases.
- No correlation (r = 0): No relationship exists between the two variables.
Significance and Applications
The correlation coefficient is extensively used in research and analysis across various fields. In AP Psychology, it is particularly valuable for:
- Testing hypotheses: Determining if there is a significant relationship between two variables.
- Predicting future outcomes: Using the correlation to forecast how one variable might influence the other.
- Identifying causal relationships: Establishing the direction and strength of the relationship between variables.
Calculating the Correlation Coefficient
The correlation coefficient can be calculated using various statistical methods, including:
- Pearson Correlation Coefficient: Suitable for linear relationships between continuous variables.
- Spearman’s Rank Correlation Coefficient: Useful when variables are ordinal or ranked.
- Kendall’s Tau Correlation Coefficient: Applicable when variables are ranked or have ties.
Interpreting the Correlation Coefficient
To interpret the correlation coefficient, it is important to consider:
- Strength of the relationship: The magnitude of ‘r’ indicates the strength of the association.
- Direction of the relationship: The sign of ‘r’ (positive or negative) indicates the direction of the association.
- Statistical significance: The p-value associated with the correlation coefficient determines its statistical significance, indicating the probability of obtaining the observed correlation by chance.
Types of Correlation Coefficients
There are several types of correlation coefficients, each suitable for specific types of data:
- Pearson Correlation Coefficient: Continuous variables with a normal distribution.
- Spearman’s Rank Correlation Coefficient: Ordinal or ranked variables.
- Kendall’s Tau Correlation Coefficient: Ranked variables with or without ties.
- Point-Biserial Correlation Coefficient: Continuous variable and a dichotomous variable.
- Phi Correlation Coefficient: Two dichotomous variables.
- Tetrachoric Correlation Coefficient: Two dichotomous variables with underlying continuous distributions.
Applications in Psychology
Correlation coefficients are used in numerous psychological research areas, including:
- Intelligence and academic achievement: Investigating the relationship between IQ and GPA.
- Personality traits and behavior: Studying the association between extroversion and social interaction.
- Mental health and well-being: Examining the correlation between depression and anxiety.
- Consumer behavior: Predicting purchase intentions based on customer demographics.
- Medical research: Determining the relationship between lifestyle factors and disease risk.
Beyond the Correlation Coefficient
While the correlation coefficient is a powerful tool, it is important to note its limitations:
- Does not establish causality: Correlation does not imply causation.
- ** Influenced by outliers:** Extreme values can skew the correlation coefficient.
- Nonlinear relationships: The correlation coefficient assumes a linear relationship, which may not be present in all cases.
Conclusion
The correlation coefficient is a fundamental concept in AP Psychology, providing a quantitative measure of the relationship between variables. Understanding its definition, calculation, and interpretation is essential for conducting accurate research and making informed decisions based on data. By utilizing various types of correlation coefficients and considering their limitations, psychologists can gain valuable insights into the complexities of human behavior and psychological phenomena.