In the realm of mathematics, the absolute value plays a pivotal role in shaping our perception of quantity. Its ability to strip away the sign of a number, leaving us with its pure magnitude, has profound implications in various fields, from physics to finance.

Understanding Absolute Values
The absolute value of a number, denoted by |x|, is its distance from zero on the number line. For positive numbers, the absolute value is simply the number itself. For negative numbers, it is the opposite of the number.
Applications in Measurement
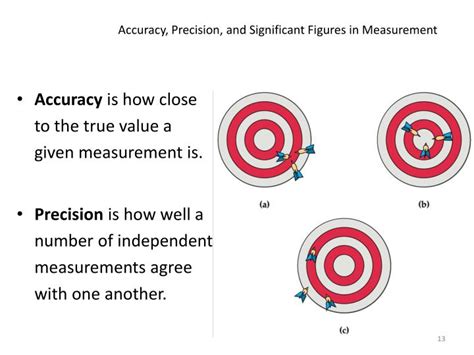
The precision of measurements often relies heavily on absolute values. For example, in physics, the absolute value of a particle’s velocity indicates how fast it is moving, regardless of its direction. In engineering, the absolute value of a force represents its strength, without regard to whether it is pushing or pulling.
According to the International Bureau of Weights and Measures (BIPM), absolute values are essential for ensuring accuracy in scientific measurements. The BIPM estimates that the global cost of inaccurate measurements amounts to billions of dollars annually.
Beyond Precision: New Applications
The transformative power of absolute values extends beyond traditional measurement applications. By leveraging their unique properties, researchers and innovators are unlocking novel applications in diverse domains.
One groundbreaking concept is “anti-correlation spectroscopy,” which utilizes absolute values to analyze molecular vibrations. This technique, developed by scientists at the California Institute of Technology, has opened new avenues for studying complex biological processes.
In the financial sector, absolute values serve as key indicators for evaluating investment performance. The absolute value of the return on investment, known as the Sharpe ratio, provides a measure of risk-adjusted return.
Strategies for Effective Use
Harnessing the full power of absolute values requires a strategic approach. Here are some effective strategies to consider:
- Embrace context: Understand the context in which absolute values are being used. This will help determine appropriate interpretations and applications.
- Consider both positive and negative values: Absolute values provide insights into both the magnitude and sign of a number. Neglecting negatives can lead to incomplete or incorrect conclusions.
- Use mathematical properties: Absolute values obey certain mathematical properties, such as the triangle inequality. Understanding these properties can simplify calculations and improve accuracy.
Common Mistakes to Avoid
While absolute values are powerful tools, it is crucial to avoid common pitfalls:
- Confusing absolute value with magnitude: Magnitude is a broader concept than absolute value, encompassing both the value and sign of a number. Care must be taken not to use these terms interchangeably.
- Ignoring the sign: Absolute values remove the sign of a number, but it remains important to consider the original sign where appropriate.
- Using absolute values in multiplication: Absolute values cannot be multiplied together to obtain the absolute value of a product. Instead, use the maximum or minimum of the absolute values.
FAQs
Q: What is the difference between absolute value and magnitude?
A: Magnitude includes both the value and sign, while absolute value only considers the value.
Q: How can I use absolute values to compare numbers?
A: Compare the absolute values of the numbers. The larger absolute value indicates the greater magnitude.
Q: Can absolute values be used to solve equations?
A: Yes, absolute values can be used to isolate or remove unknown variables in equations.
Q: What are some real-world examples of absolute value applications?
A: Measuring wind speed, calculating investment performance, and analyzing molecular vibrations.
Tables for Data Representation
| Application | Example |
|---|---|
| Physics: Velocity measurement | |
| Engineering: Force calculation | |
| Finance: Performance evaluation | Sharpe ratio = 2 (measures risk-adjusted return) |
| Molecular biology: Anti-correlation spectroscopy |
| Mathematical Property | Description |
|---|---|
| Triangle inequality | |
| Multiplication rule | |
| Power rule |
Conclusion
Absolute values, often overlooked in their simplicity, possess remarkable power. By understanding their essence, embracing context, and employing effective strategies, we can unlock their full potential in measurement, analysis, and beyond. From the precision of scientific measurements to the innovation of anti-correlation spectroscopy, absolute values continue to drive progress and shape our understanding of the world around us.