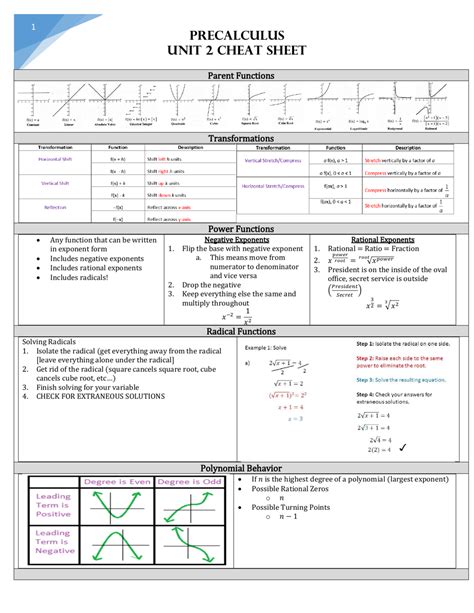
Navigating the complexities of precalculus can be overwhelming, but armed with this comprehensive cheat sheet, you’ll have an invaluable resource at your disposal. This guide covers the essential concepts, formulas, and techniques you need to succeed in your precalc studies.

Trigonometry
-
Sine, Cosine, Tangent:
- sin(θ) = opposite/hypotenuse
- cos(θ) = adjacent/hypotenuse
- tan(θ) = opposite/adjacent
- Pythagorean Identity: sin²(θ) + cos²(θ) = 1
-
Trigonometric Identities:
- cos²(θ) = 1 – sin²(θ)
- tan²(θ) + 1 = sec²(θ)
-
Special Angles:
- sin(0°) = 0, cos(0°) = 1, tan(0°) = 0
- sin(90°) = 1, cos(90°) = 0, tan(90°) = undefined
- Unit Circle: A circle with radius 1 where the coordinates (cos(θ), sin(θ)) represent the point on the circle at angle θ.
Algebra
- Polynomial Division: Use long division or synthetic division to divide polynomials.
-
Factoring: Factor polynomials using various methods:
- Common Factoring
- Trinomial Factoring
- Quadratic Formula
-
Logarithms:
- logₐ(b) = c means a^c = b
- logₐ(ab) = logₐ(a) + logₐ(b)
-
Exponential Functions:
- y = a^x, where a > 0 and a ≠ 1
- y = e^x, where e ≈ 2.718
Analytic Geometry
- Slope-Intercept Form: y = mx + b
- Point-Slope Form: y – y₁ = m(x – x₁)
- Distance Formula: Distance between (x₁, y₁) and (x₂, y₂) = sqrt((x₂ – x₁)² + (y₂ – y₁)²)
- Circle Equation: (x – h)² + (y – k)² = r², where (h, k) is the center and r is the radius.
-
Functions:
- Domain: The set of possible input values
- Range: The set of possible output values
- Graph: A visual representation of the function
Limits and Continuity
- Limits: The value that a function approaches as the input gets closer to a specific value.
- Continuity: A function is continuous if it has no breaks or jumps at a point.
- One-Sided Limits: The limit as the input approaches a value from either the left or the right.
Common Mistakes to Avoid
- Confusing sine, cosine, and tangent.
- Forgetting the Pythagorean Identity.
- Not using the correct factoring techniques.
- Misapplying the logarithm properties.
- Making errors in algebraic manipulations.
FAQs
- What are the most important formulas to know in precalc?
- Trigonometric identities, Pythagorean Identity, slope-intercept form, distance formula, logarithm properties.
- How do I prepare for a precalc test?
- Review the material regularly, use practice problems, and seek help from your teacher or a tutor.
- What are the best resources for precalc?
- Textbooks, online videos, practice websites, and tutor.
- How can I improve my problem-solving skills in precalc?
- Practice regularly, break down complex problems, and analyze your mistakes to learn from them.
- What careers use precalculus?
- Engineering, physics, computer science, finance, data analysis.
- What are some real-world applications of precalc?
- Modeling projectile motion, calculating the arc length of bridges, predicting the trajectory of a spacecraft.
Tables
-
Trigonometric Values:
| Angle | sin | cos | tan |
|—|—|—|—|
| 0° | 0 | 1 | 0 |
| 30° | 1/2 | sqrt(3)/2 | sqrt(3)/3 |
| 45° | sqrt(2)/2 | sqrt(2)/2 | 1 |
| 60° | sqrt(3)/2 | 1/2 | sqrt(3) |
| 90° | 1 | 0 | undefined | -
Algebraic Identities:
| Identity | Formula |
|—|—|
| Commutative Property of Addition | a + b = b + a |
| Associative Property of Addition | (a + b) + c = a + (b + c) |
| Distributive Property | a(b + c) = ab + ac |
| Square of a Binomial | (a + b)² = a² + 2ab + b² |
| Difference of Squares | a² – b² = (a + b)(a – b) | -
Logarithms:
| Property | Formula |
|—|—|
| Product Rule | logₐ(ab) = logₐ(a) + logₐ(b) |
| Quotient Rule | logₐ(a/b) = logₐ(a) – logₐ(b) |
| Power Rule | logₐ(a^n) = n logₐ(a) |
| Change of Base | logₐ(b) = logc(b)/logc(a) | -
Limits:
| Limit | Condition | Value |
|—|—|—|
| lim_(x->a) f(x) = L | x approaches a from both sides | f(a) = L |
| lim_(x->∞) f(x) = L | x approaches infinity | f(x) approaches L as x gets very large |
| lim_(x->-∞) f(x) = L | x approaches negative infinity | f(x) approaches L as x gets very small |