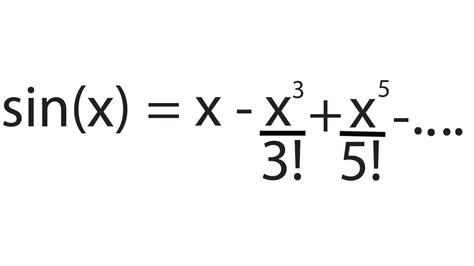The Taylor series, named after the renowned mathematician Brook Taylor, provides a powerful tool for approximating functions as infinite sums of terms. Among the most fundamental functions in mathematics, the sine function plays a vital role in various scientific and engineering disciplines. Understanding the Taylor series for sine is crucial for efficiently solving complex problems and gaining insights into the underlying mathematical concepts.

Significance of the Taylor Series for Sine
The Taylor series for sine offers numerous advantages in practical applications:
- Convergence: The Taylor series converges rapidly for values of x close to zero, making it an effective method for approximating sine values.
- Approximation Accuracy: By including more terms in the series, the approximation becomes increasingly accurate, allowing for precise calculations.
- Analytic Insights: The Taylor series reveals the relationship between the sine function and its derivatives, providing insights into the function’s behavior.
Derivation of the Taylor Series for Sine
The Taylor series for a function f(x) is expressed as:
f(x) = f(a) + f'(a)(x-a) + (f''(a)/2!)(x-a)^2 + (f'''(a)/3!)(x-a)^3 + ...
where f'(a), f”(a), f”'(a), … represent the first, second, third, … derivatives of f(x) evaluated at x = a.
To derive the Taylor series for sine, we first evaluate the derivatives:
- f(x) = sin(x)
- f'(x) = cos(x)
- f”(x) = -sin(x)
- f”'(x) = -cos(x)
- …
Substituting x = 0 and the derivatives into the Taylor series formula, we obtain:
sin(x) = sin(0) + cos(0)x + (-sin(0)/2!)x^2 + (-cos(0)/3!)x^3 + ...
Simplifying the expression further:
sin(x) = x - x^3/3! + x^5/5! - x^7/7! + ...
This is the Taylor series for the sine function centered at x = 0.
Applications of the Taylor Series for Sine
The Taylor series for sine finds applications in various fields, including:
- Numerical Analysis: Taylor series is used to approximate complex functions in numerical simulations and data analysis.
- Calculus: The Taylor series can be leveraged to evaluate integrals and derivatives of functions.
- Physics: The Taylor series is employed to analyze periodic phenomena such as wave motion and harmonic oscillators.
- Engineering: The Taylor series is utilized for designing control systems and modeling dynamic systems.
Key Terms and Concepts
- Convergence Radius: The radius of convergence for a Taylor series is the maximum distance from the center point (a) to which the series converges.
- Lagrange Remainder: The Lagrange remainder term represents the error due to truncating the Taylor series after a finite number of terms.
- Order of Approximation: The order of approximation refers to the number of terms included in the Taylor series, determining the accuracy of the approximation.
Common Mistakes to Avoid
- Overestimating Convergence Radius: Assuming that the Taylor series converges for all values of x can lead to inaccuracies. Determine the convergence radius to ensure the validity of the approximation.
- Truncating Too Soon: Truncating the Taylor series after a few terms can result in insufficient accuracy. Consider the order of approximation and the desired level of precision.
- Ignoring the Remainder Term: Neglecting the Lagrange remainder term can introduce significant errors in the approximation. Quantify the error to assess the adequacy of the approximation.
Why the Taylor Series for Sine Matters
The Taylor series for sine is a fundamental tool for understanding the sine function and its behavior. It provides an effective method for approximating sine values with varying degrees of accuracy. By understanding the Taylor series, engineers, scientists, and mathematicians can efficiently solve complex problems and gain insights into the intricate world of mathematics.