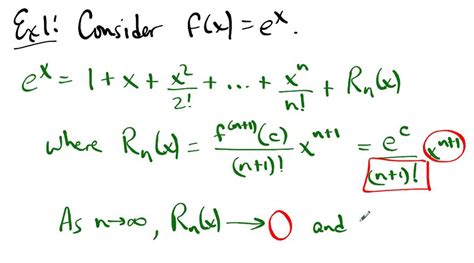Taylor series, named after the renowned mathematician Brook Taylor, are powerful mathematical tools that represent a function as an infinite sum of terms. These series are particularly useful for approximating functions that are difficult to evaluate directly. However, for Taylor series to be meaningful, they must converge to the function they represent. The radius of convergence determines the range of values for which the Taylor series converges.

What is the Radius of Convergence?
The radius of convergence (R) is a positive real number that defines the interval of convergence for a Taylor series. It is the distance from the center of convergence to the nearest point where the series diverges. If |x| < R, the Taylor series converges; if |x| > R, the Taylor series diverges.
Determining the Radius of Convergence
The radius of convergence can be calculated using various methods, including the ratio test and the root test.
Ratio Test
Let f(x) be the function represented by the Taylor series. The ratio test states that the Taylor series converges if the limit of the absolute value of the ratio of consecutive terms is less than 1:
lim (|a_{n+1}/a_n|) = L < 1
where an is the n-th term of the Taylor series. The radius of convergence is then given by:
R = 1/L
Root Test
The root test is another method for determining convergence. It states that the Taylor series converges if the limit of the n-th root of the absolute value of the n-th term is less than 1:
lim (|a_n|^(1/n)) = L < 1
The radius of convergence is then calculated as:
R = 1/L
Applications of Taylor Series with Radius of Convergence
Taylor series have numerous applications in various scientific and engineering disciplines:
-
Approximating Functions: Taylor series are used to approximate functions that are difficult to evaluate directly, such as trigonometric functions, exponential functions, and logarithmic functions.
-
Solving Differential Equations: Taylor series can be used to solve differential equations by representing the unknown function as a Taylor series and substituting it into the differential equation.
-
Numerical Analysis: Taylor series are used in numerical analysis for interpolation, extrapolation, and integration.
-
Signal Processing: Taylor series can be used in signal processing to analyze signals and extract information.
-
Chaos Theory: Taylor series are used in chaos theory to study complex dynamical systems and predict their behavior.
Innovative Word: "Convergeance"
In the context of Taylor series, we propose the term "convergeance" to describe the process of determining the radius of convergence and ensuring that the Taylor series converges to the function it represents. Convergeance is a critical step in using Taylor series effectively, and it involves both theoretical understanding and computational skills.
Tips for Convergeance
Effective convergeance strategies include:
-
Choose an Appropriate Center of Convergence: The center of convergence should be chosen carefully to maximize the radius of convergence.
-
Use High-Order Terms: Including more terms in the Taylor series generally increases the radius of convergence.
-
Apply Convergence Tests: The ratio test or root test should be used to determine the radius of convergence and ensure convergence.
-
Consider Analytic Functions: Analytic functions have a Taylor series that converges everywhere, so the radius of convergence is infinite.
Common Mistakes to Avoid
Common mistakes to avoid in convergeance include:
-
Ignoring Convergence: Neglecting to check for convergence can lead to erroneous results.
-
Using Inaccurate Tests: Applying the wrong convergence test or using it incorrectly can result in misleading conclusions.
-
Choosing an Improper Center of Convergence: An inappropriate center of convergence can significantly reduce the radius of convergence.
-
Truncating the Taylor Series Prematurely: Using too few terms in the Taylor series can compromise accuracy and lead to divergence.
Conclusion
The radius of convergence is a crucial factor in understanding and using Taylor series effectively. By applying convergence tests, selecting appropriate centers of convergence, and considering analytic functions, researchers and practitioners can harness the power of Taylor series to approximate functions, solve differential equations, and explore complex phenomena. The concept of convergeance provides a framework for ensuring that Taylor series converge to the functions they represent, making them an invaluable tool in various scientific and engineering applications.
Useful Tables
Table 1: Examples of Common Functions and Their Radius of Convergence
| Function | Radius of Convergence |
|---|---|
| ex | ∞ |
| sin(x) | ∞ |
| cos(x) | ∞ |
| ln(1+x) | 1 |
Table 2: Strategies for Increasing the Radius of Convergence
| Strategy | Effect |
|---|---|
| Choose a center of convergence closer to the desired region of convergence | Increases the radius of convergence |
| Use more terms in the Taylor series | Generally increases the radius of convergence |
| Use convergence tests to determine the optimal number of terms | Ensures convergence and maximizes the radius of convergence |
| Consider analytic functions | Have an infinite radius of convergence |
Table 3: Applications of Taylor Series with Radius of Convergence
| Application | Example |
|---|---|
| Function approximation | Approximating ex using the first 5 terms of its Taylor series |
| Differential equation solving | Solving a first-order differential equation using a Taylor series expansion |
| Numerical integration | Approximating the integral of a function using its Taylor series |
| Signal processing | Analyzing signals using the Fourier series, which is based on Taylor series expansion |
Table 4: Common Mistakes to Avoid in Convergeance
| Mistake | Consequence |
|---|---|
| Ignoring convergence | Erroneous results |
| Using inaccurate tests | Misleading conclusions |
| Choosing an improper center of convergence | Reduced radius of convergence |
| Truncating the Taylor series prematurely | Compromised accuracy and divergence |