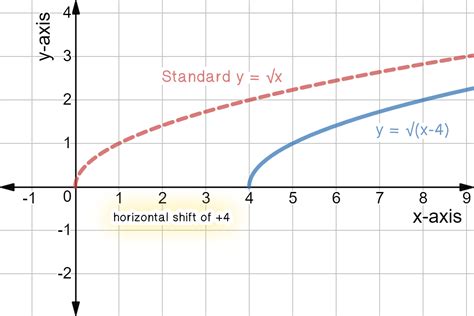
The graph of the square root function, denoted as √x, is a fundamental concept in mathematics with far-reaching applications across various fields. This iconic curve has been a subject of fascination and study for centuries, inspiring the development of new ideas and groundbreaking discoveries.

Understanding the Square Root Function
The square root of a number is the value that, when multiplied by itself, gives the original number. The square root function is defined as the inverse of the squaring operation, i.e., √(x^2) = x.
Graph of Square Root x: A Visual Representation
The graph of the square root function is a curve that opens upward and extends infinitely to the right. The curve starts at the origin (0,0) and continuously rises at an increasing rate of change.
Properties of the Square Root Function
The square root function possesses several key properties:
- Non-negative Output: The square root of any non-negative number is always non-negative.
- Symmetrical: The function is symmetrical about the y-axis, meaning that √(x) = -√(-x).
- Monotonic: The square root function is increasing, meaning that as x increases, √x also increases.
- Concave Up: The graph of the function is concave up, indicating that it curves upward throughout its entire domain.
Applications of the Square Root Function
The square root function finds widespread applications in various disciplines, including:
- Physics: Calculating projectile trajectories, fluid flow rates, and electrical power dissipation.
- Mathematics: Determining the length of diagonals in triangles, proving geometric theorems, and solving quadratic equations.
- Computer Science: Creating algorithms for searching, sorting, and data compression.
- Engineering: Designing bridges, optimizing structural stability, and predicting material behavior.
- Biology: Modeling cell growth rates, estimating population densities, and analyzing enzymatic reactions.
Benefits of Understanding the Square Root Function
Understanding the square root function provides numerous benefits:
- Problem-Solving: Enables the solution of complex problems involving square roots in various contexts.
- Model Development: Facilitates the development of mathematical models that accurately represent real-world phenomena.
- Analytical Skills: Sharpens analytical thinking and enhances critical reasoning abilities.
- STEM Education: Strengthens foundational knowledge for students pursuing careers in science, technology, engineering, and mathematics.
Importance of the Square Root Function in Society
The square root function is an essential mathematical tool that underpins countless technological advancements and societal progress:
- Engineering Marvels: The function plays a crucial role in the design and construction of skyscrapers, airplanes, and bridges.
- Medical Breakthroughs: Square roots are used in medical imaging, drug dosage calculations, and genetic analysis.
- Economic Modeling: The function helps economists forecast market trends, predict consumer behavior, and optimize investment strategies.
- Environmental Sustainability: Square roots are employed in calculating pollution levels, estimating carbon footprints, and designing renewable energy systems.
Potential Applications in Uncharted Waters
Harnessing the power of the square root function can lead to innovative applications in emerging fields, such as:
- Quantum Computing: Optimizing algorithms for quantum computers and solving complex mathematical problems.
- Artificial Intelligence: Creating algorithms for image recognition, natural language processing, and machine learning.
- Healthcare: Developing personalized medical treatments and predicting disease risk based on genetic data.
- Space Exploration: Calculating trajectories for space probes and optimizing fuel efficiency in interplanetary travel.
Conclusion
The graph of square root x is an iconic mathematical representation that encapsulates both beauty and utility. Its properties, applications, and benefits make it an indispensable tool for scientists, engineers, economists, and anyone seeking to understand the complexities of our world. As society continues to progress, the square root function will undoubtedly play an even more pivotal role in shaping future innovations and discoveries.
Tables
Table 1: Key Properties of the Square Root Function
| Property | Description |
|---|---|
| Non-negative Output | √(x) ≥ 0 for x ≥ 0 |
| Symmetry | √(x) = -√(-x) |
| Monotonic | The function is increasing. |
| Concave Up | The graph curves upward throughout its domain. |
Table 2: Applications of the Square Root Function in Various Disciplines
| Discipline | Applications |
|---|---|
| Physics | Projectile trajectories, fluid flow rates, electrical power dissipation |
| Mathematics | Triangle diagonals, geometric theorems, quadratic equations |
| Computer Science | Searching, sorting, data compression |
| Engineering | Bridge design, structural stability, material behavior |
| Biology | Cell growth rates, population densities, enzymatic reactions |
Table 3: Benefits of Understanding the Square Root Function
| Benefit | Value |
|---|---|
| Problem-Solving | Enables the solution of complex problems |
| Model Development | Facilitates the development of accurate models |
| Analytical Skills | Sharpens critical reasoning abilities |
| STEM Education | Enhances foundational knowledge in science and math |
Table 4: Potential Applications of the Square Root Function in Emerging Fields
| Field | Applications |
|---|---|
| Quantum Computing | Optimizing quantum algorithms, solving complex problems |
| Artificial Intelligence | Image recognition, natural language processing, machine learning |
| Healthcare | Personalized medical treatments, disease risk prediction |
| Space Exploration | Space probe trajectories, fuel efficiency optimization |