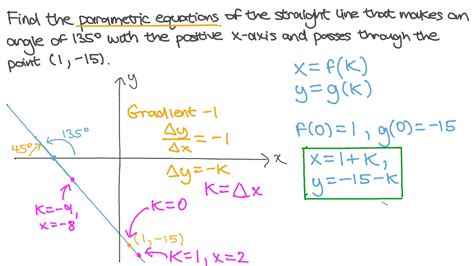Parametric equations offer a powerful tool for describing complex curves in mathematical terms. By parameterizing a curve, we can express its coordinates as functions of a single parameter, thereby gaining valuable insights into its shape and behavior.

Why Use Parametric Equations?
Parametric equations provide several key advantages over traditional Cartesian equations:
-
Embracing Curves of Arbitrarily Complex Shapes: Parametric equations can describe curves that cannot be easily expressed using standard algebraic equations, such as circles, ellipses, and spirals.
-
Describing Motion in Space and Time: Parametric equations prove essential in describing the motion of objects in space over time. Physicists and engineers often use them to model projectile trajectories, planetary orbits, and fluid flow patterns.
-
Simplifying Differential Equations: Parametric equations can simplify the analysis of differential equations, making them invaluable in studying topics such as vibrating strings, heat transfer, and wave propagation.
How to Find Parametric Equations
To find the parametric equations of a curve, we need to identify two functions, (x(t)) and (y(t)), that express the x and y coordinates of each point on the curve as a function of the parameter (t).
Example: Circle
Consider a circle of radius (r) centered at the origin. We can parameterize this circle using the trigonometric functions:
x(t) = r * cos(t)
y(t) = r * sin(t)
where (t) varies from 0 to (2\pi).
Example: Parabola
A parabola opening upwards with vertex at the origin can be parameterized as:
x(t) = t^2
y(t) = t
where (t) ranges from (-\infty) to (\infty).
Types of Parametric Equations
There are various types of parametric equations, depending on the nature of the curve:
Plane Curves
- Explicit Parametric Equations: The coordinates are given directly as functions of the parameter, as in the examples above.
- Implicit Parametric Equations: The curve is defined by an equation involving both (x) and (y), with the parameter (t) serving as a hidden variable. For example, the equation (x^2 + y^2 – t^2 = 0) defines a circle parametrically.
Space Curves
- Regular Parametric Curves: The curve can be traced without cusps or sharp corners. The tangent vector is always nonzero.
- Singular Parametric Curves: There are points on the curve where the tangent vector is zero, resulting in cusps or sharp corners.
Applications of Parametric Equations
The applications of parametric equations extend far beyond abstract mathematics. They find practical use in diverse fields:
Computer Graphics
- 3D Modeling: Parametric equations form the basis of many 3D modeling software programs. They allow designers to create complex shapes and surfaces.
- Animation: Animators use parametric equations to control the movement of objects over time, creating realistic and fluid motions.
Engineering
- Robotics: Engineers utilize parametric equations to program the movements of robotic arms, ensuring accurate and precise motion.
- Fluid Dynamics: Parametric equations describe the flow of fluids, helping engineers design efficient and effective systems.
Physics
- Projectile Motion: Physicists use parametric equations to model the trajectories of projectiles, considering factors like gravity and initial velocity.
- Planetary Orbits: Astronomers employ parametric equations to track the orbits of planets and celestial bodies, predicting their positions over time.
Digital Signal Processing
- Fourier Analysis: Parametric equations form the foundation of Fourier analysis, a technique used to decompose signals into their frequency components.
- Wavelet Analysis: Wavelet analysis relies on parametric equations to represent and manipulate signals at different scales.
Conclusion
Parametric equations offer a powerful tool for representing and analyzing complex curves. They have wide-ranging applications, from computer graphics and engineering to physics and digital signal processing. Mastering parametric equations unlocks new possibilities for understanding and manipulating the world around us.