Introduction
In the realm of physics and mathematics, the interplay between implicit derivatives and particle motion is a captivating symphony. This harmonious union unfolds a profound comprehension of how physical systems evolve over time. By leveraging the power of implicit differentiation, we unlock the secrets of particle motion, delving into its intricacies and gaining valuable insights.

What are Implicit Derivatives?
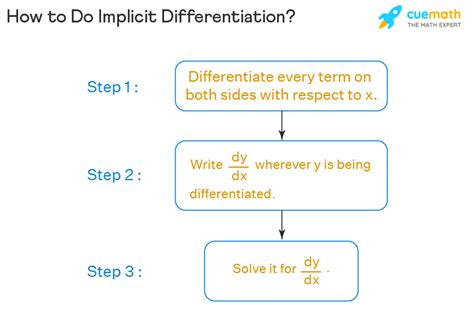
Implicit derivatives are a mathematical tool used to determine the rate of change of a dependent variable with respect to an independent variable when the former is defined implicitly. They arise when the relationship between the variables is expressed in an equation that does not explicitly solve for the dependent variable.
Consider the implicit equation:
F(x, y) = 0
where F is a differentiable function of two variables, x and y. To find the derivative of y with respect to x, we use the chain rule and implicit differentiation:
\frac{dy}{dx} = -\frac{F_x}{F_y}
where F_x and F_y represent the partial derivatives of F with respect to x and y, respectively.
Applications of Implicit Derivatives in Particle Motion
Implicit derivatives find widespread use in particle motion, providing a powerful means to analyze and predict the behavior of particles under various forces.
Velocity and Acceleration
In one-dimensional motion, the velocity of a particle is given by the derivative of its position function x(t) with respect to time t:
v = dx/dt
Similarly, acceleration is the derivative of velocity with respect to time:
a = dv/dt = d^2x/dt^2
Using implicit differentiation, we can determine the velocity and acceleration of a particle even when its position function is not explicitly given.
Trajectory Analysis
The trajectory of a particle is the path it follows through space. By analyzing the implicit equation of the trajectory, we can gain insights into the shape and characteristics of the path. For example, if the equation is a circle, we know that the particle is moving along a circular path.
Force and Motion
Implicit derivatives play a crucial role in understanding the relationship between force and motion. Newton’s second law states that the force acting on a particle is equal to the mass of the particle times its acceleration:
F = ma
By combining this equation with implicit differentiation, we can determine the force acting on a particle even when its acceleration is not explicitly given.
Tables of Applications
Applications in Physics
| Application | Implicit Equation | Insight |
|---|---|---|
| Circular Motion | x^2 + y^2 = r^2 | Particle moves in a circle of radius r |
| Projectile Motion | y = -0.5gt^2 + v0t | Velocity and height of a projectile |
| Simple Harmonic Motion | x = A cos(ωt + φ) | Frequency and amplitude of oscillation |
Applications in Other Fields
| Application | Implicit Equation | Insight |
|---|---|---|
| Population Growth | P = P0e^(kt) | Exponential growth of a population |
| Chemical Kinetics | A + B → C | Reaction rate of a chemical reaction |
| Economic Modeling | Y = f(K, L) | Relationship between output and capital and labor |
Strategies for Finding Implicit Derivatives
- Identify the implicit relationship. Clearly state the equation that defines the implicit relationship.
- Differentiate both sides with respect to the independent variable. Use the chain rule and implicit differentiation techniques.
- Solve for the derivative of the dependent variable. Isolate the desired derivative using algebraic operations.
Tips and Tricks
- Practice: Solving numerous problems will enhance your ability to apply implicit derivatives confidently.
- Use technology: Graphing calculators or software can aid in visualizing the implicit function and verifying your results.
- Check your work: Differentiate the resulting equation implicitly to ensure it satisfies the original implicit relationship.
Step-by-Step Approach
To find the implicit derivative of a function using the chain rule:
- Differentiate the outer function with respect to the independent variable.
- Multiply by the derivative of the inner function with respect to the dependent variable.
Creative New Word: “Particlepathy”
Particlepathy describes the study of particle motion using implicit derivatives and other mathematical techniques. This emerging field opens new avenues for exploring and predicting the behavior of particles in complex systems.
Conclusion
Implicit derivatives and particle motion form a synergistic partnership, empowering us to delve into the intricacies of physical phenomena. By harnessing their combined power, we gain a deeper understanding of how particles move in space and time. From analyzing trajectories to predicting forces, implicit derivatives are an indispensable tool in the study of particle motion and beyond.