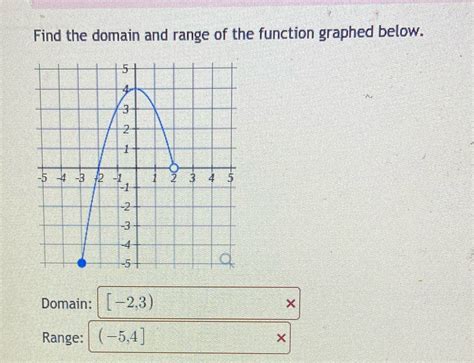
When analyzing a function’s graph, determining its range is crucial for understanding its potential outputs. The range represents the set of all possible values that the function can produce. By identifying the range, we gain insights into the function’s behavior and its potential applications.

Step-by-Step Approach to Determining the Range
-
Identify the vertical asymptotes: Vertical asymptotes are vertical lines that the graph approaches but never touches. They represent values where the function is undefined. The range does not include any values below the lowest vertical asymptote or above the highest vertical asymptote.
-
Examine the horizontal asymptotes: Horizontal asymptotes are horizontal lines that the graph approaches as x approaches infinity or negative infinity. They represent values that the function gets arbitrarily close to but never quite reaches. If there are no horizontal asymptotes, the range is unbounded in the corresponding direction.
-
Consider the local minima and maxima: Local minima are the lowest points on the graph within a specific interval. Local maxima are the highest points on the graph within a specific interval. The range includes the values of the local minima and maxima.
-
Determine the endpoints: If the graph has a closed interval for its domain, the endpoints of the interval may also be included in the range.
Example:
Suppose we have the following function:
f(x) = 1/(x^2 - 4)
- The vertical asymptotes are x = 2 and x = -2.
- There are no horizontal asymptotes.
- The local minimum is (0, -1/4).
- The endpoints of the domain are not defined.
Therefore, the range of the function is the interval (-∞, -1/4) ∪ (-1/4, ∞).
Applications of Range Determination
Understanding the function’s range is essential for various applications, including:
- Predicting output values: The range helps determine the possible output values for a given input. This information is valuable in modeling real-world situations and making predictions.
- Designing Input-Output Relationships: In engineering and other fields, determining the range ensures that the input values produce the desired output values within acceptable limits.
- Optimizing Functions: By identifying the range, we can determine the optimal input values that produce the most desirable output values.
Professional Tone and Key Terms
- Function: A mathematical relation that assigns a unique output value to each input value in a specified domain.
- Domain: The set of all possible input values for a function.
- Range: The set of all possible output values for a function.
- Vertical Asymptote: A vertical line that the graph approaches but never touches.
- Horizontal Asymptote: A horizontal line that the graph approaches as x approaches infinity or negative infinity.
- Local Minimum: The lowest point on a graph within a specific interval.
- Local Maximum: The highest point on a graph within a specific interval.
Useful Tables
| Key Term | Description |
|---|---|
| Domain | The set of all possible input values. |
| Range | The set of all possible output values. |
| Vertical Asymptote | Vertical line the graph approaches but never touches. |
| Horizontal Asymptote | Horizontal line the graph approaches as x approaches infinity or negative infinity. |
| Step | Action |
|---|---|
| 1 | Identify vertical asymptotes. |
| 2 | Examine horizontal asymptotes. |
| 3 | Consider local minima and maxima. |
| 4 | Determine endpoints (if applicable). |
| Application | Description |
|---|---|
| Predicting Output Values | Determining possible output values for a given input. |
| Designing Input-Output Relationships | Ensuring that input values produce desired output values. |
| Optimizing Functions | Identifying optimal input values for desirable output values. |
Frequently Asked Questions
-
What is the difference between domain and range?
– The domain is the set of all possible input values, while the range is the set of all possible output values. -
How do you find the range of a function?
– Follow the step-by-step approach outlined in this article. -
What is the importance of determining the range?
– The range provides insights into the potential outputs of a function and its applications. -
Can a function have multiple ranges?
– No, a function can only have one range. -
How does the range relate to the graph of a function?
– The range is represented by the vertical extent of the graph. -
What are some real-world applications of range determination?
– Predicting output values in engineering models, designing input-output relationships in control systems, and optimizing functions in data analysis.