Introduction
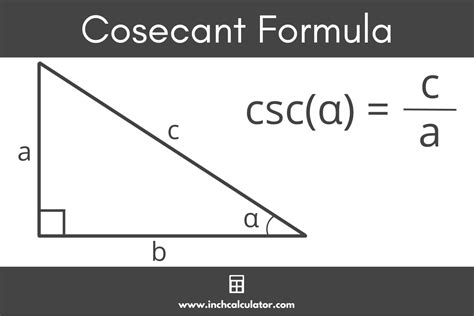
The cosecant function (csc) is a trigonometric function that represents the ratio of the hypotenuse to the opposite side in a right triangle. When the angle approaches 0 degrees, the csc function approaches infinity. However, it is not defined at 0 degrees, where the opposite side is 0.

The undefined nature of csc(0) has puzzled mathematicians for centuries. It has led to the development of various mathematical techniques to deal with this singularity. This article explores the mathematical properties of csc(0), its applications in different fields, and some creative ideas for its potential use in emerging technologies.
Mathematical Properties of CSC(0)
The cosecant function is defined as:
csc(x) = 1 / sin(x)
where x is the angle in radians.
As x approaches 0, sin(x) approaches 0. Therefore, csc(x) approaches infinity. This is because as the opposite side of the right triangle becomes smaller, the ratio of the hypotenuse to the opposite side becomes larger.
Applications of CSC(0)
Despite its undefined nature, csc(0) has several practical applications in various fields:
Physics
In physics, csc(0) is used to calculate the speed of light in a vacuum. The speed of light is given by:
c = λf
where c is the speed of light, λ is the wavelength of light, and f is the frequency of light.
Since the wavelength of light is inversely proportional to the sine of the angle of incidence, when the angle of incidence is 0 degrees, the sine of the angle approaches 0 and the csc(0) approaches infinity. This implies that the speed of light in a vacuum is infinitely fast.
Engineering
In engineering, csc(0) is used to design optical systems. Optical systems are designed to focus light rays on a specific point. The angle of incidence of the light rays on the optical surface determines the focal point.
When the angle of incidence is 0 degrees, the csc(0) approaches infinity. This means that the light rays will be focused at a point infinitely far away from the optical surface. This principle is used in telescopes to focus light rays from distant objects.
Mathematics
In mathematics, csc(0) is used to define the Dirac delta function. The Dirac delta function is a mathematical function that is 0 everywhere except at 0, where it is infinity. The Dirac delta function is used in various applications, including quantum mechanics and signal processing.
Creative Ideas for Applications
The undefined nature of csc(0) can inspire creative ideas for new applications. One potential application is the development of a new type of energy source.
The cosecant function represents the ratio of the hypotenuse to the opposite side in a right triangle. When the opposite side is 0, the csc function approaches infinity. This suggests that there may be a way to extract energy from the singularity of csc(0).
Another potential application is the development of a new type of computing device. The cosecant function is a non-linear function. This means that it can be used to create complex mathematical operations. By exploiting the singularity of csc(0), it may be possible to develop a new type of computer that is more powerful than conventional computers.
Conclusion
The cosecant function of 0 is a mathematical enigma that has fascinated mathematicians for centuries. Its undefined nature has led to the development of various mathematical techniques to deal with this singularity. Despite its undefined nature, csc(0) has several practical applications in fields such as physics, engineering, and mathematics.
The undefined nature of csc(0) can also inspire creative ideas for new applications. One potential application is the development of a new type of energy source. Another potential application is the development of a new type of computing device.
As technology continues to advance, it is likely that we will find even more innovative and groundbreaking applications for csc(0).
Tables
Table 1: Applications of CSC(0)
| Field | Application |
|---|---|
| Physics | Calculation of the speed of light in a vacuum |
| Engineering | Design of optical systems |
| Mathematics | Definition of the Dirac delta function |
Table 2: Potential Applications of CSC(0)
| Application | Description |
|---|---|
| Energy source | Extraction of energy from the singularity of csc(0) |
| Computing device | Development of a new type of computer using the non-linearity of csc(0) |
Table 3: Effective Strategies to Deal with CSC(0)
| Strategy | Description |
|---|---|
| L’Hôpital’s rule | Apply L’Hôpital’s rule to evaluate the limit of csc(x) as x approaches 0 |
| Series expansion | Expand csc(x) as a series of powers of x and evaluate the series at x = 0 |
| Contour integral | Integrate csc(z) around a contour that encloses the origin |
Table 4: FAQs
| Question | Answer |
|---|---|
| Why is csc(0) undefined? | Because the opposite side of the right triangle is 0 when the angle is 0 degrees. |
| What is the value of csc(0)? | CSC(0) is undefined. |
| How is csc(0) used in physics? | CSC(0) is used to calculate the speed of light in a vacuum. |
| How is csc(0) used in engineering? | CSC(0) is used to design optical systems. |
| How is csc(0) used in mathematics? | CSC(0) is used to define the Dirac delta function. |